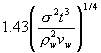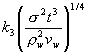A ferramenta numérica utilizada para definir os limites dos estuários Portugueses Sistema MOHID. O desenvolvimento deste sistema iniciou-se em na década de 80 (Neves, 1985), tendo vindo a ser objecto de sucessivos aperfeiçoamentos na sequência da respectiva aplicação a diferentes projectos científicos e tecnológicos. Actualmente este sistema de modelação matemática pode ser classificado com um dos mais elaborados entre os sistemas existentes deste tipo, nomeadamente no que respeita às inovações na coordenada vertical e à programação robusta e fiável.

O sistema MOHID foi programado recorrendo a programação orientada por objectos, utilizando o ANSI Fortran 95. O sistema se encontra dividido em diferentes módulos, podendo cada um deles ser entendido com um modelo específico, sendo no entanto o sistema composto por um único ficheiro executável.

A utilização do ANSI Fortran 95 garante a independência do sistema MOHID face ao sistema operativo no qual se pretende executar o modelo (Windows, Linux, Unix, etc.) e uma fácil implementação do código em qualquer ambiente. O tempo de execução do programa (tempo simulado versus tempo da unidade central de processamento) varia em função da malha de cálculo e do passo de tempo utilizado. No entanto, a possibilidade de correr os vários módulos (hidrodinâmica, turbulência, deriva, etc.) com passos de tempo diferentes permite uma optimização do tempo de cálculo necessário para a execução das simulações.

Tirando partido das novas funcionalidades do Fortran 95, o sistema utiliza a alocação dinâmica da memória, se tornando assim mais versátil, optimizando o uso dos recursos do computador e permitindo utilizar um único executável independentemente das dimensões do domínio de cálculo a utilizar.

O sistema MOHID pode ser divido em quatro grandes classes:

q duas gerem as propriedades do escoamento não turbulentas (ex. velocidade, elevação, fluxos de água) e turbulentas (viscosidade turbulenta, difusividade, energia cinética turbulenta, comprimentos de mistura). A evolução das propriedades em ambas as classes é calculada num referencial euleriano pelo método dos volumes finitos.

q as outras duas classes gerem as propriedades da água (ex. salinidade, temperatura, densidade, sedimentos coesivos, parâmetros de qualidade). Uma destas classes resolve a evolução das propriedades também num referencial euleriano pelo método dos volumes finitos. A outra classe simula a evolução das propriedades num referencial lagrangeano, esta classe é a base do módulo de deriva.

A técnica de volumes finitos consiste em aplicar as leis (físicas, químicas e biológicas), que regem os processos que se pretendem simular, directamente a um volume de controlo na forma de uma divergência de um fluxo. Como consequência, este método garante automaticamente a conservação de massa das propriedades simuladas (Adcroft et al., 1997).

A classe responsável pela evolução das propriedades da água num referencial lagrangeano evoluiu de um modelo de traçadores lagrangeanos utilizado nas versões anteriores do MOHID (Leitão, 1997). Hoje em dia o modelo lagrangeano pode ser utilizado para simular uma diversidade de processos de transporte e de qualidade da água bem como a deriva de manchas de petróleo (Silva, 1997).

As quatro grandes classes acima referidas se encontram repartidas por mais de 40 módulos que constituem o sistema MOHID perfazendo um total mais de 140 mil linhas de código.

A programação orientada por objectos utilizada na programação do modelo torna a sua utilização, tal como a sua expansão, muito robusta (Miranda et al., 2000). Este tipo de programação tem provado ser uma metodologia muito útil no desenvolvimento de programas complexos, em especial para aqueles que têm por objectivo simular problemas “do mundo real” (Decyk et al., 1998), dos quais a modelação de processos marinhos ou estuarinos se constituem como exemplos. A comunicação entre os módulos é feita numa base de cliente/servidor garantindo assim o encapsulamento da informação de cada módulo (Duffy, 1995).

Ao longo da sua existência, o modelo MOHID tem vindo a ser utilizado em inúmeros casos de estudo entre os quais se podem encontrar zonas com características muito diferentes como sejam o caso do oceano profundo (casos do Atlântico Nordeste, no âmbito do projecto Omex, e do mar Mediterrâneo, no âmbito do projecto EuroModel), zonas fluviais e estuarinas, zonas costeiras, lagoas e albufeiras.

2 Módulo Hidrodinâmico

O módulo hidrodinâmico do sistema Mohid resolve as equações primitivas do movimento no espaço tridimensional. A discretização espacial destas equações é feita utilizando uma técnica de volumes finitos a qual permite a utilização de um sistema de coordenadas verticais genérico. A discretização temporal é baseada na utilização de um esquema semi-implícito.

O modelo permite a consideração de condições de fronteira abertas ou fechadas. As condições de fronteira abertas podem ser do tipo nível imposto, radiativas ou um misto das duas.

A versatilidade do módulo hidrodinâmico permite que se proponha esta como a única ferramenta para simular o escoamento em todos os locais onde serão elaborados cenários de derrames independentemente da complexidade da respectiva geometria.

No texto que se segue é apresentada uma descrição do modelo incluindo as equações resolvidas, o fecho turbulento, as condições de fronteira aberta e a geometria vertical do modelo.

2.1 Equações resolvidas

As equações resolvidas pelo módulo hidrodinâmico têm todas por base a equação que descreve na forma integral da evolução de uma variável genérica P, no interior de um volume de controle:

( 1)

sendo A a superfície que define a fronteira do volume controle e V o integral de superfície decorresponde ao fluxo da propriedade P através de A.

O módulo hidrodinâmico tem como objectivo simular a evolução das propriedades do escoamento. As velocidades segundo X e Y (horizontais) são umas dessas propriedades, as quais são calculadas com base na equação (1) e admitindo que:

As forças gravíticas englobam as forças de atração gravítica exercidas sobre o volume de controle em estudo pelo planeta Terra 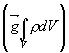, pela Lua e pelo Sol (potencial da maré).

O potencial de maré é um termo que adquire importância em domínios de grandes dimensões, da ordem das centenas de km, sendo resolvido com base na formulação proposta por Choi et al. (1997).

As forças de pressão e as forças viscosas são exercidas sobre a superfície fronteira do volume de controle e resultam da interação deste com o meio envolvente. As forças de pressão são normais à superfície de fronteira enquanto que as forças viscosas podem ser subdivididas em tangenciais e normais.

No que diz respeito às forças viscosas tangenciais é necessário definir condições de fronteira no fundo e à superfície. No fundo é utilizada uma lei quadrática em que a tensão de corte é igual ao coeficiente Chezy vezes o quadrado da velocidade. Na superfície, caso um dos agentes forçadores seja o vento, a tensão de corte é a tensão de corte do vento caso contrário o seu valor é nulo.

Outra propriedade fundamental a ter em consideração é a nível da superfície livre cuja evolução é calculada com base na equação (1) admitindo que o meio é 2D, isto é, a sua evolução só é condicionada pelos fluxos de água. Neste caso os termos da equação se podem escrever na forma:

P = r

Fontes – Poços = Descargas + Precipitação - Evaporação

A equação (1) se torna então numa equação de conservação de massa 2D:

Descargas + Precipitação – Evaporação (2)

Ao contrário da equação anterior em que a propriedade transportada era a incógnita, aqui a propriedade é conhecida (r) e a incógnita é o próprio volume de controle.

Uma vez que se trata de um abordagem 3D é ainda necessário especificar uma equação para o cálculo da velocidade vertical, a qual é obtida a partir da equação de conservação de massa anteriormente descrita admitindo a hipótese hidrostática.

2.2 Principais aproximações

A equação (1) aplicada à conservação de quantidade de movimento é válida para um referencial fixo. No entanto, o referencial natural, a Terra, está em permanente rotação, sendo o efeito desta rotação sobre o escoamento usualmente contabilizado na forma de uma força inercial denominada força de Coriólis.

Outra aproximação, usualmente efectuada na aplicação da lei de conservação de quantidade de movimento a escoamentos oceânicos e costeiros, explora o fato das variações de densidade da água nestes casos ser muito pequena, menos de 3%. Neste caso a densidade pode ser considerada constante para o cálculo da sua massa e forças de inércia, excepto para as forças que são função da aceleração da gravidade. A esta simplificação chama-se aproximação de Boussinesq.

Uma terceira simplificação adoptada tem em consideração que, no oceano e em águas costeiras, as escalas na vertical são pequenas e, consequentemente, o escoamento tem de uma forma geral velocidades muito baixas nessa direcção. Para além da dimensão das escalas verticais a estratificação vertical de densidade estável tem também um papel importante, porque tende a inibir qualquer movimento vertical por acção da impulsão. As acelerações verticais são baixas tal como as forças viscosas. O fluido por sua vez, no que diz respeito aos movimentos verticais, se comporta como se estivesse num equilíbrio estático. Nestas condições é válida a hipótese hidrostática, isto é, é possível desprezar todos os termos de inércia e admitir que o gradiente de pressão vertical está em equilíbrio com a força da gravidade. A pressão, no caso da hipótese hidrostática, é então apenas função da profundidade e do gradiente vertical de densidade.

Na discretização do termo de pressão se optou pela divisão deste numa componente barotrópica e outra baroclínica. A primeira contabiliza o efeito do gradiente de nível sobre a pressão, enquanto a segunda contabiliza o efeito do gradiente de densidade. Esta divisão permite correlacionar directamente a variação da superfície livre com a pressão (barotrópica). Desta forma a superfície livre pode ser utilizada para calcular o volume de controle e simultaneamente servir como estimativa da pressão barotrópica. Por outro lado, se podem aplicar métodos numéricos diferentes a cada um dos termos.

Na perspectiva da oceanografia, esta divisão pode também ser encarada como uma divisão de modos: a pressão barotrópica força o modo externo, responsável por simular as ondas gravíticas da superfície livre (cf. Figura 1) que apresentam uma celeridade muito superior à dos modos internos. Estes últimos, do ponto de vista físico têm um número infinito e são forçados pela pressão baroclínica, sendo a sua fase visível a propagação das chamadas ondas internas (cf. Figura 2).

Figura 1- Propagação de uma onda de superfície livre simulada pelo sistema Mohid. Neste caso esquemático a onda é imposta num pequeno canal situado no lado direito do domínio e radiada pelas outras três fronteiras.

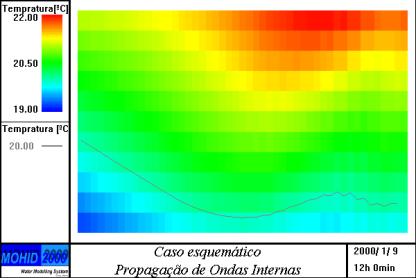
Figura 2- Propagação de uma onda interna simulada pelo sistema Mohid. Simulação da propagação de ondas internas ao longo de um canal com 50 km e 1000 m de profundidade com uma estratificação inicial linear de temperatura (24ºC à superfície e 4 ºC no fundo). A figura mostra a variação da isolinha dos 20 ºC ao longo de todo o canal e entre os 150 e 250 m de profundidade. O canal tem fronteira aberta (radiação) do lado direito e fechada do lado esquerdo, as ondas internas são formadas extraindo, nas três primeiras células a contar do lado esquerdo, calor da superfície a uma taxa de 300 W/m².

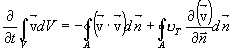
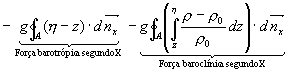
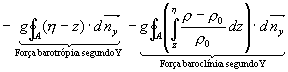
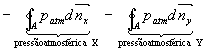
A consideração das aproximações à lei de conservação de quantidade de movimento, apresentadas anteriormente, dão origem à equação 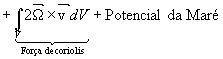( 3).

( 3)

O módulo hidrodinâmico resolve assim a equação de conservação de quantidade de movimento 3D ( 3) para calcular as componentes horizontais da velocidade e uma equação de conservação de massa ( (2), para um meio 2D, para calcular a variação da superfície livre no tempo. Finalmente resolve mais uma vez a equação (2), agora para um meio 3D, para calcular a velocidade vertical do escoamento.

A densidade é calculada com base na equação de estado para a salinidade e a temperatura (Leendertsee e Liu, 1978):

( 4)

Os valores de salinidade e de temperatura são calculados com base num módulo independente da hidrodinâmica responsável pela evolução relativa a um referencial euleriano de todas as propriedades da água o qual resolve a equação (1) aplicada a um meio 3D.

A temperatura e a salinidade podem ser valores constantes ou evoluir no tempo devido ao efeito do transporte por parte do escoamento de descargas pontuais, de fluxos à superfície, de trocas de calor no caso da temperatura (radiação solar, radiação infravermelha, calor latente e sensível) e trocas de massa no caso da salinidade (evaporação/precipitação).

2.3 Fecho turbulento

A resolução numérica das equações do módulo hidrodinâmico além de ser discreta no espaço também o é no tempo. Por este motivo, o módulo hidrodinâmico resolve na realidade as equações apresentadas anteriormente com base numa decomposição à Reynolds.

Esta decomposição pode ser perspectivada como uma filtragem temporal, em que os valores instantâneos das propriedades ()são substituídos por quantidades médias () mais flutuações turbulentas ().

A integração temporal da equação ( 3) permite escrevê-la em termos de valores médios surgindo, devido aos efeitos não lineares, termos adicionais (tensores de Reynolds). Estes termos representam a contribuição do transporte turbulento para o campo médio e podem ser vistos como o transporte das flutuações do campo variável em estudo pelas flutuações do campo da velocidade.

Levanta-se assim um novo problema usualmente designado por “fecho da teoria da turbulência”. Existem diversos métodos de resolver este problema sendo comum admitir que este novo termo é proporcional ao gradiente da propriedade média transportada, ou seja:

( 5)

A variável u_T é designada por viscosidade turbulenta. Nos casos em que o meio possa ser considerado isotrópico se pode admitir que u_T é constante. Caso contrário é necessário calcular para cada uma das direcções um valor, .

Na maioria dos casos se admite , uma vez que na horizontal os processos normalmente se podem considerar homogéneos. A grande diferença reside nas escalas características das direcções horizontal e vertical. Nesta perspectiva, o coeficiente de viscosidade turbulenta pode ser dividido em viscosidade turbulenta horizontal e vertical, .

Uma vez que se admitiu que o novo termo tem uma natureza matemática semelhante ao termo das forças viscosas, a sua ordem de grandeza é facilmente comparável. As escalas normalmente resolvidas pelos modelos hidrodinâmicos são da ordem dos metros, a que corresponde uma viscosidade turbulenta várias ordens de grandeza superiores à viscosidade molecular, pelo que as forças viscosas podem ser consideradas desprezáveis.

Na horizontal o sistema Mohid permite três opções de parametrização da viscosidade turbulenta nomeadamente: valor constante, Smagorinsky e bi-harmónico.

O fecho turbulento vertical é feito com base o módulo de turbulência do modelo GOTM (General Turbulence Ocean Model). Neste módulo se podem encontrar um conjunto de diferentes modelos para a descrição das trocas turbulentas nas camadas de mistura. Todos os modelos usam o principio de viscosidade turbulenta, que permite obter os coeficientes de troca turbulenta em função de propriedades do escoamento médio.

Entre os modelos introduzidos no GOTM, os fechos de segunda ordem de duas equações (k-e e Mellor-Yamada) são os que descrevem mais realisticamente a turbulência nas camadas limite de superfície e fundo, com um detalhe que permite a sua utilização num modelo tridimensional sem um custo computacional elevado.

Os modelos k-e e Mellor-Yamada mais evoluídos no modelo GOTM (e portanto no sistema MOHID) diferem da versão standard na escolha dos parâmetros nas equações de transporte que controlam a transição a condições de estratificação estável e na utilização de funções de estabilidade, numericamente estáveis, que consideram mais correlações no fecho da turbulência. Isto permite uma melhor descrição da camada de mistura para distintos escoamentos como tem sido demostrado em diversas aplicações a distintos ambientes tanto em plataformas continentais como em estuários e em oceano aberto.

O modelo também incorpora parametrizações dos coeficientes turbulentos no interior do oceano, isto é, onde os processos de estratificação dominam sobre as tensões de corte criadas na superfície e no fundo. Para mais informação sobre as aplicações e os avanços teóricos no modulo de turbulência do modelo GOTM pode consultar-se a página web (http://www.gotm.net).

Os modelos de turbulência de duas equações no sistema MOHID (k-e e Mellor-Yamada) calculam os coeficientes de troca turbulenta (para o momento n_tpara o momento e n^’_t para o calor) a partir da expressão:

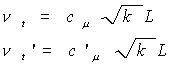(6)

onde k representa a energia cinética turbulenta, L a escala de comprimento característica dos movimentos turbulentos e c_me c´_m , as funções de estabilidade para o momento e os escalares, respectivamente.

A energia cinética turbulenta é calculada com base numa equação de transporte:

(7)

onde a evolução temporal da TKE é um balanço dum termo difusivo, um termo de produção pela tensão de corte do escoamento médio P, um termo B , que dá conta das trocas entre TKE e energia potencial e um termo disipativo e que é sempre um poço e representa a dissipação da TKE em energia térmica.

No modelo de Mellor-Yamada o comprimento característico da turbulência é calculado mediante uma equação de transporte da forma:

(8)

e no modelo k-e calcula a dissipação da TKE, que se relaciona com o comprimento turbulento pela expressão:

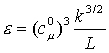(9)

A equação de transporte para a dissipação da TKE é da forma:

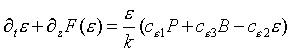(10)

Embora os modelos standard k-e e Mellor-Yamada possam ser utilizados no MOHID, a eleição do valor de c_e₃ e as funções de estabilidade para as quais se obtêm resultados mais realistas em distintas situações são diferentes das standard, permitindo uma melhoria sensível na descrição da dinâmica das camadas de mistura.

2.4 Discretização Espacial

A maior parte dos modelos hidrodinâmicos utilizam na discretização espacial das equações o método das diferenças finitas ou o métodos dos elementos finitos. Um método menos divulgado é o dos volumes finitos. Neste caso o ponto de partida são equações aplicadas a volumes de controle tal como foram apresentadas anteriormente. Desta forma a malha é definida explicitamente e as equações são resolvidas sempre da mesma forma independentemente da geometria das células. Uma vez que as equações são sempre resolvidas na forma de uma divergência de um fluxo, este método garante a conservação das propriedades transportadas (Ferziger e Perić, 1995 e Vinokur, 1989).

Apesar de, no módulo hidrodinâmico aqui apresentado, se ter optado por volumes finitos com uma malha estruturada por uma questão de simplicidade de discretização e eficiência de cálculo, esta metodologia pode ser aplicada facilmente a malhas não estruturadas. Esta metodologia foi utilizada por Chippada et al. (1998) para simular processos costeiros tendo utilizado uma malha não estruturada de volumes de controle na forma de triângulos.

2.4.1 Discretização Vertical

Tal como na horizontal, na discretização vertical é comum a utilização de transformação de coordenadas para optimizar a precisão da malha. Na vertical este problema é ainda mais importante porque os gradientes são normalmente muito superiores. Uma discretização grosseira na vertical pode dar origem a excesso de difusão numérica e pode tornar impraticável, por exemplo, a simulação do efeito da estratificação sobre um escoamento.

Uma das principais características dos modelos oceânicos e costeiros de diferenças finitas é a abordagem que adoptam para a discretização vertical. As discretizações mais conhecidas são: a sigma, a isopícnica e a cartesiana. A partir desta característica é possível antever que, por exemplo, um modelo sigma (ex: POM, SCRUM) é uma boa ferramenta para o estudo de meios bem misturados que sigam a topografia do fundo, mas já não são em meios estratificados com fortes gradientes de topografia.

Um modelo de coordenadas isopícnicas pode ser uma boa solução para simular meios estratificados onde o escoamento seja forçado pela densidade. Neste tipo de discretização as camadas da malha coincidem com linhas de iso-densidade tendo por objectivo de minimizar a difusão numérica entre camadas, partindo do pressuposto que o escoamento se faz preferencialmente ao longo destas linha e que a estratificação vertical inibe trocas significativas entre camadas. Em regiões influenciadas pelo fundo, pela inércia ou em presença de escoamentos secundários o campo de velocidades possui uma componente importante na direcção perpendicular às isopícnicas (linhas de igual densidade), contrariando os pressupostos deste modelo.

Por fim a malha cartesiana pode ser uma boa solução nos casos em que as duas discretizações anteriores falham, como seja por exemplo o escoamento ao longo do talude da plataforma continental (Neves et al., 2000). Neste caso a influência da topografia é caracterizada por fortes gradientes e o escoamento não segue as isopícnicas.

Tendo em consideração a variabilidade de comportamentos que é possível encontrar na natureza, se pode dizer que na maioria das aplicações não existe uma discretização que seja a que melhor se adapte à simulação de todo o domínio, verificando-se que, por vezes, a melhor solução seria discretizar de forma diferente vários sectores do domínio.

Os modelos dupla-sigma (Deleersnijder e Beckers, 1992 e Santos, 1995) constituem uma tentativa de resposta para este tipo de problemas. Neste caso a coluna de água é dividida em dois domínios sigma: um do fundo até uma profundidade constante, normalmente a base da camada de mistura, e outro, por cima, onde é aplicada uma segunda discretização sigma, que só acompanha o fundo nas pequenas profundidades, evitando assim uma malha muito distorcida, em especial, nas zonas profundas (> 1000 m). Ao evitar esta distorção o modelo minimiza a mistura vertical associada à difusão numérica horizontal.

Este tipo de modelos que combinam diferentes discretizações, apesar de poderem representar uma solução para alguns problemas, continuam no entanto a apresentar pouca flexibilidade.

A solução mais eficiente será então recorrer a um modelo que não dependa de um tipo limitado de discretizações e que permita ao utilizador criar novas discretizações sem muito esforço.

Os modelos de volumes finitos permitem uma grande flexibilidade, ao nível da discretização espacial, uma vez que a geometria é introduzida duma forma explícita através das áreas e volumes de cada célula. Esta versatilidade permite subdividir o domínio tanto na horizontal como na vertical, em zonas com diferentes discretizações (cf. Figura 3).

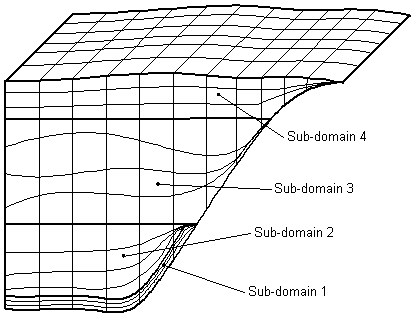
Figura 3 – Malha ilustrativa das potencialidades de discretização vertical do sistema Mohid.

Esta metodologia possibilita igualmente o desenvolvimento, sem muito esforço, de coordenadas verticais alternativas que melhor se adaptem a um caso particular. Este é o caso da coordenada Lagrangeana que foi desenvolvida para minimizar as trocas entre camadas (Figura 4), sendo possível assim reduzir ao mínimo a difusão numérica associada ao transporte horizontal (Neves et al., 2000).

As coordenadas cartesianas tradicionais consideram cada camada com uma espessura constante ao longo de todo o domínio. Esta regra rígida levanta problemas na discretização do fundo. Uma solução alternativa é a utilização do conceito de células cortadas (shaved cells), que consiste em garantir que, junto ao fundo, a espessura da camada é igual à profundidade menos o nível da face mais próxima do fundo (Figura 4b). Este tipo de metodologia é extremamente simples de implementar em modelos de volumes finitos (Adcroft e Marshall, 1997, Martins et al., 2000).


(a)	(b)

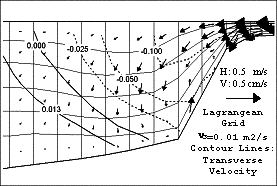
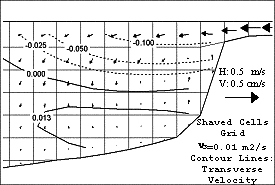
Figura 4 – Cortes verticais mostrando escoamentos secundários num talude. A figura a) apresenta resultados obtidos com uma malha Lagrangeana que foi incializada com uma configuração de malha sigma enquanto a figura b) representa o mesmo escoamento com uma malha cartesiana com células cortadas junto ao fundo.

Tendo por objectivo a resolução de problemas específicos, e tirando partido da flexibilidade do sistema Mohid neste aspeto, foram implementadas no sistema outras discretizações inovadoras, como seja o caso da discretização designada de “Harmónica”, a qual foi implementada para permitir correr o sistema Mohid em Albufeiras. Nestes casos se verificam situações em que a superfície livre, num ano seco, pode variar mais 30 m.

Tendo em conta estas oscilações extremas foi desenvolvida uma coordenada que é inicializada como se fosse cartesiana e quando o nível da albufeira começa a descer a espessura da camada diminui à mesma velocidade até atingir uma espessura mínima quando essa é atingida, o processo repete-se para a camada logo abaixo e assim sucessivamente. Quando o nível da albufeira sobe as camadas que são expandidas pela ordem inversa com que foram contraídas. Esta nova coordenada, permite de uma forma eficiente, manter a estratificação da albufeira evitando todos os problemas de difusão numérica associados à coordenada sigma (Braunschweig, 2001).

Outro exemplo inovador é uma coordenada que melhora a parametrização do atrito no fundo, a que se chamou de “espessura fixa”. Neste caso, admite-se que camadas de espessura constante acompanham o fundo. Este tipo de coordenada é, utilizada junto ao fundo e complementada por outro tipo de discretização vertical até à superfície livre. Esta coordena permite que a distância à parede (fundo) das velocidades calculadas mais perto do fundo seja sempre constante tornando o calculo do atrito mais consistente e preciso.

A flexibilidade do sistema Mohid ao nível da discretização vertical permite a respectiva utilização tanto em ambientes oceânicos (cf. Figura 5), como escoamentos estuarinos (cf. Figura 6), em circulação em albufeiras (cf. Figura 7) ou até processos de pequena escala como seja a dispersão de plumas térmicas (cf. Figura 8).

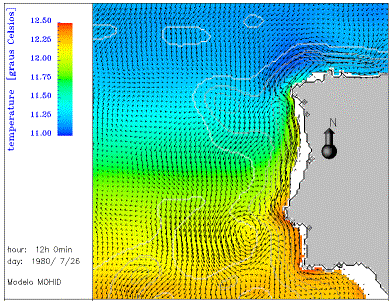
Figura 5 – Campo de correntes no Atlântico. Resultados produzidas no âmbito do projecto cientifico europeu OMEX (Coelho et al., in press).

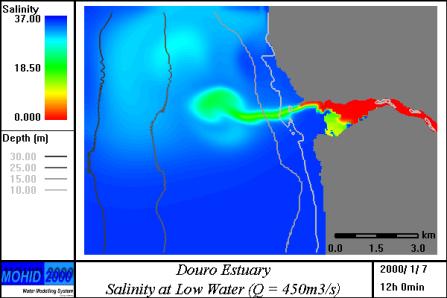
Figura 6 – Campo de salinidades no estuário do Douro para uma situação de caudal médio e baixa mar.

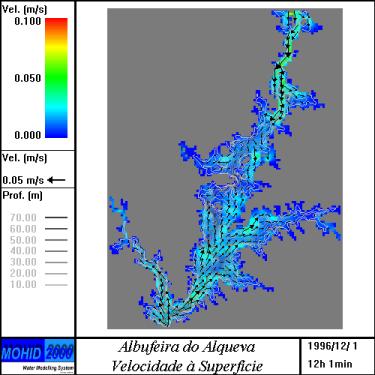
Figura 7 – Escoamento na futura Albufeira do Alqueva. Quando a barragem desta albufeira estiver construída o Alqueva será o maior lago artificial da Europa.

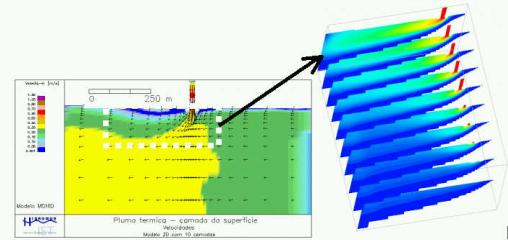
a) b)

Figura 8 – Simulação da dispersão da pluma térmica duma central termoeléctrica situada perto de Lisboa. a) Campo de velocidades à superfície b) campo vertical de temperatura.

2.4.2 Discretização Horizontal

A resolução horizontal do sistema Mohid é variável em sua extensão, permitindo a simulação mais detalhada das correntes nas zonas dos terminais e consequentemente das trajectórias das manchas de óleo (cf. Figura 9).

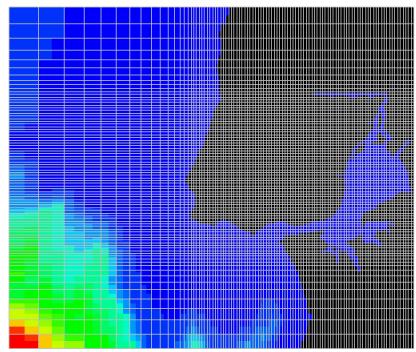
Figura 9- Exemplo de aplicação de passo variável ao estuário do Tejo (Portugal).

O modelo utiliza uma malha que na classificação proposta por Arakawa e Lamb (1977) corresponde à malha C (cf. Figura 10). Este tipo de abordagem evita médias no cálculo dos gradientes de pressão (barotrópica e baroclínica) e da divergência de fluxos (continuidade: nível e traçadores).

Figura 10 – Classificação de malhas 2D descentradas segundo Arakawa e Lamb (1977).

A distribuição dos pontos de cálculo adotada para o cálculo das propriedades do escoamento (h, v_x, v_y v_z), minimiza o número de interpolações, atribuindo maior importância ao cálculo dos gradientes de pressão (barotrópica e baroclínica) e de divergência de fluxos (continuidade: nível e traçadores). Implica no entanto a execução de médias para calcular o termo de coriólis. Em qualquer dos casos, a precisão da solução só está comprometida quando o passo da malha não permite resolver o raio de deformação interno de Rossby (~40 km a 30º de latitude). Esta escala espacial corresponde à distância horizontal ao longo da qual um fluido estratificado em rotação é afectado quando perturbado. (11)

(11)

sendo c é a celeridade da perturbação num meio estratificado.

Usualmente os modelos globais utilizam uma malha do tipo B, uma vez que, mesmo recorrendo a super-computadores a precisão destes modelos não é suficiente para resolver o raio de deformação interno de Rossby. Existem já modelos que têm uma precisão de 0.2º graus (Kantha and Clayson, 2000) antevendo, que num futuro próximo, mesmo os modelos globais tenderão a utilizar malhas do tipo C. Este tipo de malha é também a ideal para acoplar o modelos hidrodinâmicos a modelos de propriedades da água uma vez que não é necessário recorrer a interpolações para calcular a divergência de fluxos.

2.5 Discretização Temporal

Os termos que condicionam a estabilidade das equações são a pressão barotrópica (ondas gravíticas), o atrito no fundo e a difusão vertical. Ao primeiro está associada uma celeridade elevada, , sendo h a profundidade e g a aceleração gravítica. A discretização do atrito levanta alguns problemas quando o gradiente de velocidade junto ao fundo é muito intenso. Por fim a difusão vertical introduz maiores dificuldades quando a discretização vertical é muito fina.

Como o objectivo de não impôr limites muito restritivos aos critérios de estabilidade foi adoptada uma discretização semi-implícita do tipo ADI “Alternante Direction Implicit”). Os três termos que apresentam mais problemas de estabilidade foram discretizados implicitamente, enquanto que para os restantes se optou por uma abordagem explícita. A vantagem de um método semi-implícito sobre um totalmente implícito é o sistema de equações resultante poder ser do tipo tridiagonal. Estes sistemas são resolvidos de uma forma muito eficiente pelo algoritmo de Thomas. Os métodos implícitos, quando aplicados a domínios 2D e 3D, dão origem a sistemas de equações esparsos, sendo por isso, necessário recorrer a métodos dispendiosos em termos de rapidez de cálculo.

O modelo prevê ainda a possibilidade de utilização, em alternativa, de dois tipos de discretizações semi-implícitas: uma que necessita da resolução de 6 equações em cada passo temporal (cf. Figura 11) conhecido pelo esquema de Leendertse (Leendertse, 1967) e outra baseada no esquema S21 (Abbott et al., 1973) que envolve a resolução de 4 equações (cf. Figura 12).

Em ambos os métodos o esquema ADI é aplicado à equação da continuidade (2D-horizontal) para calcular a elevação da superfície livre. Basicamente, substituí-se alternadamente todo (Leendertse) ou parte (S21) do integral da velocidade numa direcção, por uma equação de conservação de quantidade de movimento, enquanto na direcção perpendicular mantêm-se a velocidade explícita.

Figura 11 – Discretização temporal do método de 6 equações proposto por Leendertse, 1967.

Figura 12 – Discretização temporal do método S21proposto por Abbott et al., 1973.

2.6 Condições de Fronteira

O modelo permite a consideração de condições de fronteira abertas e fechadas. As primeiras são usualmente utilizadas para definir a interacção do módulo hidrodinâmico com outras massas de água, enquanto as segundas são utilizadas para definir a linha de costa e os processos de cobertura e descobertura em zonas intertidais.

As condições de fronteira aberta podem ser divididas em dois tipos: passivas e activas. Estas últimas são conhecidas à priori, isto é, são impostas e não calculadas pelo modelo. Um exemplo deste tipo de fronteira é a imposição de uma curva de maré para simular a hidrodinâmica de um estuário ou a imposição da vazão de um rio para simular uma cunha salina. As condições de fronteira passivas dependem da solução interna e têm como principal objectivo deixar sair perturbações geradas dentro do domínio. As fronteiras radiativas são um exemplo deste tipo de condição de fronteira, sendo utilizadas em diversos tipos de aplicação: ondas de vento, escoamentos oceânicos e costeiros.

As fronteiras fechadas podem-se dividir em fixas e móveis. As primeiras são utilizadas para definir a linha de Costa, enquanto as segundas são extremamente úteis para definir processos de cobertura e descobertura em zonas intertidais. Tanto ao nível de fluxo de massa como de quantidade de movimento optou-se, por defeito, por impor fluxo nulo ao longo destas fronteiras fechadas.

2.6.1 Fronteiras abertas

Desde o início do desenvolvimento do sistema Mohid, em 1985, as condições de fronteira aberta foram eleitas como um dos principais temas de investigação. Este é um tema complexo e exige um acompanhamento constante do estado da arte e investigação das várias soluções.

Diversas teses de doutoramento e mestrado (Aires, 1995, Silva, 1991, Villarreal 2001) têm sido e se encontram ainda a ser desenvolvidas no seio da equipe responsável pelo desenvolvimento e manutenção do sistema Mohid, das quais resultaram a publicação de diversos artigos científicos que abordam esta temática (Neves e Silva, 1991, Aires e Neves, 1991, Villarreal et al., in press, Coelho et al., in press).

Ao longo do tempo tem sido efectuada uma actualização constante das diferentes metodologias propostas na bibliografia que provaram ser robustas em casos reais. A experiência acumulada tem mostrado que não existe uma solução universal e que, em cada caso, é necessário testar diferentes soluções, optando pela que menos perturbe a solução e simultaneamente não deixe o modelo divergir.

A metodologia para definir condições de fronteira abertas é extremamente versátil. Uma forma que o utilizador tem de garantir que a simulação não tende a divergir da solução conhecida, é definindo uma solução exterior (ou de referência) e fornecê-la ao módulo hidrodinâmico na entrada de dados. Esta solução exterior pode ser definida de uma forma contínua para cada ponto de cálculo recorrendo a campos de propriedades definidos em ficheiros ASCII, que podem ser constantes ou variáveis no tempo.

Outra hipótese é definir a solução em alguns pontos, e o módulo hidrodinâmico durante o Run interpolar a solução para os pontos fronteira. Esta é a metodologia utilizada na imposição da maré. Esta abordagem tem a vantagem de minimizar a entrada de dados. A informação pode ser dada na forma duma série temporal ou na forma de componentes harmónicas no caso da maré.

A solução exterior pode ser definida com base em medidas feitas especificamente para o trabalho de modelação ou a partir de base de dados construídas por organismos especializados em recolha e processamento de medidas. Caso não existam fontes locais de medidas de salinidade, de temperatura, de ventos e maré, as fontes alternativas usualmente utilizadas pelo grupo de utilizadores do Mohid são bases de dados disponíveis na internet que disponibilizam informação para todo o mundo como é o caso da NOAA (Levitus e Boyer, 1994 e Levitus et al., 1994) cujos dados climatológicos de salinidade e temperatura são extremamente úteis, porque permitem determinar um campo de velocidades e níveis, admitindo que a hipótese geostrófica é válida.

A metodologia normalmente utilizada para se obter este escoamento consiste em considerar uma profundidade de movimento nulo (Paillet e Mercier, 1997, Arhan et al, 1994).

Com base na equação do vento térmico (12) e admitindo que a velocidade a uma determinada profundidade é nula é possível obter o perfil de velocidade acima dessa mesma profundidade.

(12)

Sabendo que a velocidade barotrópica é a média do perfil de velocidades é possível obter o gradiente da superfície da relação geostrófica integrada na vertical. Os dados de ventos podem ser utilizados não só como forçamento interno mas também para definir a solução exterior, a partir da deriva de Ekman ou da solução de Severdrup. Uma fonte de ventos para qualquer ponto do globo podem ser os modelos atmosféricos globais, como é o caso do modelo do ECMWF (European Center for Medium-Range Weather Forecasts - Trenberth et al., 1990). Como solução de recurso podem ser utilizados os ventos climatológicos propostos por Hellerman e Rosenstein (1983).

No caso da maré podem sert utilizados os resultados do modelo global de maré FES95.2 (Le Provost et al., 1998). Este modelo não é mais que um modelo hidrodinâmico de elementos finitos FES94.1 (Le Provost et al., 1994) ao qual foi adicionado um módulo de assimilação de dados. A assimilação de dados é efectuada a partir da solução obtida do modelo empírico CSR2.0 da universidade de Texas para os oceanos Atlântico, Índico e Pacífico. A principal razão apontada para os erros do modelo puramente hidrodinâmico FES94.1 são o desconhecimento da batimetria em muitas zonas do Globo.

Os resultados do modelo FES95.2 disponíveis na internet (ftp://spike.cst.cnes.fr/pub/techine/tide/fes95.2.1) têm uma precisão de 0.5ºx0.5º graus. Estes resultados referem-se a 26 componentes de maré para todo o mundo. As 8 principais componentes de maré são calculadas directamente pelo modelo hidrodinâmico: K1, O1, Q1, M2, S2, N2, K2 e 2N2 em que somente as duas últimas não são corrigidas por assimilação de dados. As outras 18 componentes de maré são obtidas a partir das oito principais. A qualidade dos resultados do modelo foi aferida por comparação com a informação medida em 95 estações espalhadas por todo o mundo.

Em alternativa, também é possível utilizar o próprio módulo hidrodinâmico para calcular a solução de referência recorrendo ao conceito de modelos encaixados (cf. Figura 13). Uma vez que toda a programação do sistema Mohid está orientada por objectos, o número de modelos encaixados que o utilizador pode definir é ilimitado. Na realidade, esta escolha está limitada à capacidade de cálculo disponível.

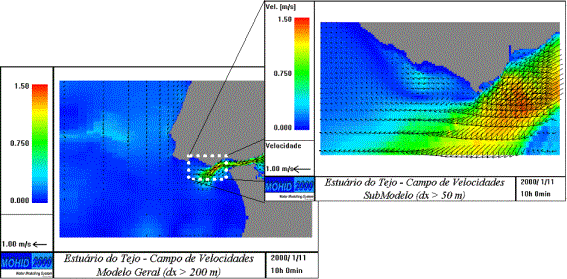
Figura 13 – Modelos encaixados aplicados ao estuário do Tejo. Estudo efetuado no âmbito do plano de monitorização da qualidade da água das praias da costa do Estoril.

Esta metodologia é extremamente poderosa, podendo ser utilizada um de dois métodos para definir a solução exterior. Um dos caminhos possíveis a seguir é definir um modelo de larga escala com um passo espacial grosseiro, onde seja relativamente fácil definir as condições de fronteira, e de seguida ir implementando modelos encaixados que, na zona de estudo, tendam a reduzir o passo da malha até se obter a precisão desejada. Esta metodologia tem como desvantagem a exigência em termos de capacidade de cálculo. O outro caminho consiste em recorrer a modelos encaixados para obter uma solução exterior que não é mais do que uma simplificação das equações primitivas. Neste caso, se pode correr em paralelo um modelo que resolva as equações primitivas e um outro que resolva, para o mesmo domínio as equações simplificadas propostas por Roed e Smedstad (1984), que não necessitam de condições fronteira, uma vez que desprezam todos os termos não lineares e os gradientes perpendiculares à fronteira. O sistema Mohid permite ao utilizador na entrada de dados anular termos das equações e assim resolver estas numa forma simplificada.

O cálculo do escoamento nas fronteiras por parte do módulo hidrodinâmico está dividido em duas etapas. Numa primeira etapa as equações primitivas são resolvidas. Neste caso a fronteira pode ser resolvida impondo a solução exterior, anteriormente referida, ou resolvendo uma equação que permite com base nas condições internas do módulo hidrodinâmico extrapolar o valor na fronteira (radiação) ou um misto das duas.

As propriedades que necessitam de condições de fronteira no módulo hidrodinâmico são, nomeadamente: os níveis, as velocidades e os traçadores (ex: temperatura e salinidade). Os níveis podem ser impostos (condição de fronteira activa) ou então, caso se opte por uma condição de radiação, existem duas possibilidades :

· Condição de fronteira de Blumberg e Kantha (1985)

· Condição de fronteira de Flather (1976)

– vector normal à fronteira

T_d– tempo de decaimento

h_ext, v_ext– nível e velocidade da solução exterior

h, v– nível e velocidade a calcular

A primeira opção tem a particularidade de ser calculada no ponto de fronteira dos níveis e, a segunda, no primeiro ponto de cálculo das velocidades. Ambas as soluções podem ser totalmente radiativas, desde que o tempo de decaimento na primeira seja infinito ou os valores exteriores no segundo caso sejam nulos, caso contrário são uma solução híbrida entre uma condição de fronteira activa e passiva.

A condição de fronteira das velocidades não é tão importante no balanço de forças, uma vez que só influencia os termos difusivo, advectivo e de Coriólis, que são termos de inércia, mas pode ser relevante em termos de estabilidade. Neste caso nos pontos fronteira é resolvida uma equação simples de radiação (Palma e Matano, 1998 e Palma e Matano, 2000):

sendo c a celeridade a que se propagam as perturbações.

Se c = 0 esta condição se torna numa condição de valor imposto. Se c = + ¥ então estamos perante uma condição de gradiente nulo.

O valor real de c é difícil de determinar porque as perturbações na componente barotrópica da velocidade se propagam a enquanto as da componente baroclínica propagam-se a uma velocidade 2 ordens de grandeza inferior (velocidade de propagação das ondas internas), usualmente assumido como sendo mas ao qual está associada uma grande incerteza. A solução é dividir na fronteira as velocidades em duas componentes aplicar a equação anterior a cada uma delas e voltar a somá-las.

Para o caso dos traçadores é resolvida uma equação de advecção que pode ou não ser corrigida com uma velocidade radiativa (Stevens 1991). Esta equação é semelhante à proposta por Blumberg e Kantha (1985) para os níveis:

Neste caso o valor de c é igual ao da componente baroclínica das velocidades, na medida em que ambos sofrem a influência da propagação de ondas internas.

A segunda etapa do cálculo dos valores na fronteira, pode ou não ser accionada pelo utilizador e consiste em, após a resolução das equações, relaxar qualquer ponto de cálculo para a solução exterior com o objectivo de não deixar a solução simulada divergir devido a pequenas inconsistências entre a solução de referência e as equações do módulo hidrodinâmico (13). Neste caso é resolvida a seguinte equação:

(13)

Neste caso P é uma propriedade genérica que pode ser o nível, uma velocidade ou um traçador, P^* é a propriedade calculada recorrendo às equações primitivas enquanto P^ext é o valor da propriedade da solução exterior e a o seu peso relativo. A condição de fronteira FRS (Flow Relaxation Scheme) proposta por Martinsen e Engedahl (1987) não é mais que aplicar esta metodologia numa faixa de dez células ao longo da fronteira admitindo que o coeficiente a tem o valor de um na fronteira e tende para zero conforme se afaste desta.

2.6.2 Fronteiras fechadas

Fisicamente existem trocas de quantidade de movimento entre a costa e o escoamento por atrito lateral. Todavia este processo é desprezável relativamente ao atrito no fundo, devido à diferença existente entre o passo espacial na horizontal e na vertical. O seu efeito do atrito lateral sobre o escoamento só será visível no escoamento para passos de malha inferior a 10 m. Nestes casos o utilizador tem que escolher a opção de não escorregamento lateral.

Como foi anteriormente referido, a fronteira móvel é uma fronteira fechada cuja posição evolui no tempo. Este tipo de fronteira é utilizada para simular zonas intertidais. Neste caso é necessário fazer uma verificação constante de todos os pontos de cálculo de velocidades que estão descobertos onde é imposta a condição de fluxo de massa e fluxo de quantidade de movimento nulos. Um ponto de cálculo das velocidades se considera descoberto se uma das seguintes condições ocorrer:

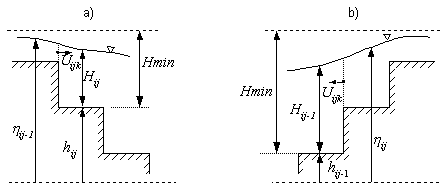
Figura 14– Condições para um ponto de cálculo de velocidades se considerar descoberto.

HMIN é a altura de coluna de água mínima, abaixo do qual se considera que um ponto de cálculo de níveis já não tem água. Este valor tem que ser suficientemente grande de modo a minimizar a criação artificial de massa mas, por outro lado, se for demasiado grande pode introduzir erros na propagação da maré nas zonas intertidais.

O ruído provocado pelas variações bruscas de velocidade nas fases de cobertura ou descobertura deve ser controlado através de uma escolha criteriosa de HMIN (Leendertse, 1970, Stelling, 1983). O valor normalmente utilizado é na ordem dos 4 cm. As outras variáveis são H_ij profundidade total (ou altura da coluna de água), h_ij profundidade (ou cota a que se encontra o fundo) e h_ij nível (ou cota a que se encontra a superfície livre utilizando um referencial simétrico ao das profundidades).

3 Módulo de Transporte Lagrangeano

Os primeiros modelos de transporte lagrangeanos de que se podem encontrar referências na bibliografia utilizavam o conceito de traçador única e exclusivamente para seguir a respectiva trajectória e, deste modo, perceber de uma forma intuitiva os mecanismos de transporte.

Nestes modelos as propriedades básicas de cada traçador eram apenas a origem e a posição espacial. Posteriormente surgiram versões mais sofisticadas, que tinham como principal objectivo o estudo do impacte em ecossistemas aquáticos de emissões pontuais antropogénicas. Nestes modelos já aparecem associadas aos traçadores novas características que incluem propriedades indicadoras da qualidade da água (ex: coliformes, petróleo, temperatura e fitoplâncton), geometria, velocidade de sedimentação e propriedades turbulentas do escoamento.

No início dos anos 80 esta nova geração de modelos lagrangeanos tornou-se numa ferramenta comum de gestão ambiental. Nesta fase eram utilizados, principalmente, para estudar a dispersão de plumas térmicas de usinas termo eléctricas e plumas de emissários (Bork e Maier-Reimer, 1978, Chin, 1985, Monteiro et. al, 1992, Monteiro e Neves, 1992, Neves e Martins, 1996). Estes casos são caracterizados por gradientes acentuados e pelas plumas terem, usualmente, uma dimensão muito inferior à área que é simulada. Neste tipo de aplicações, a aproximação lagrangeana constitui uma boa solução, pois permite manter gradientes elevados uma vez que esta metodologia não possui os problemas de difusão numérica que caracteriza os modelos eulerianos.

O aumento exponencial da capacidade de cálculo dos computadores que se tem verificado nos últimos anos veio permitir que os modelos de traçadores lagrangeanos venham a ser utilizados para simular processos cada vez mais complexos, nomeadamente: o transporte de sedimentos Kelsey et. al, (1994), a dispersão de petróleo Shiau (1991), Mansur e Price (1992), produção primária Woods and Onken (1982), Dippner (1993), Rodrigues et. al (1996), Rodrigues and Neves, (1996)

O modelo lagrangeano tridimensional, aqui apresentado, foi inicialmente desenvolvido para ser acoplado à primeira versão do modelo hidrodinâmico Mohid (Neves, 1985) que era um modelo bidimensional. Numa segunda fase foram sendo adicionadas novas potencialidades permitindo a simulação de processos tais como descargas de águas residuais, emissão pontual de sedimentos (ex: rios e material dragado), trajectórias de manchas de petróleo e cálculo de tempos de residência.

Numa terceira fase o modelo foi generalizado para ser facilmente acoplado tanto a modelos 2D como 3D (Leitão, 1997). Neste modelo, os traçadores (ou partículas) possuem seis características principais: coordenadas espaciais (x, y, z), velocidade horizontal/vertical, tempo durante o qual o traçador mantém a velocidade, velocidade de sedimentação, massa e volume. Para cada umas destas propriedades é resolvida uma equação de evolução. A massa pode ser um array de mais de 30 propriedades (ex: nutrientes, fitoplancton, matéria em suspensão).

3.1 Deslocamento dos traçadores

As coordenadas espaciais são calculadas a partir da definição de velocidade:

A qual é resolvida com base num um método explícito simples:

A aplicação de métodos de ordem mais elevada, implica a utilização de procedimentos iterativos. O método de Heun utilizado por Monteiro (1995) corresponde a um esquema de previsão-correcção de dois níveis temporais, com um grau de precisão de 2 ^a ordem no tempo. Costa (1991) concluiu que a adopção de esquemas de ordem mais elevada só é necessária quando as linhas de corrente apresentam uma curvatura acentuada e o passo temporal é elevado. Para a maioria dos escoamentos naturais, a precisão, associada ao método explícito, é suficiente para se obterem bons resultados.

Para calcular a velocidade em qualquer ponto do domínio, é utilizada uma interpolação linear (cf. Figura 15), também neste caso se poderia optar por um método de interpolação mais preciso, como a interpolação bilinear utilizada por Monteiro (1995), embora este aumento de precisão torne o algoritmo mais lento.

Figura 15- Cálculo da velocidade média dos traçadores.

Ás velocidades U_x e U_x+dx, segundo x, nas faces 1 e 2 podem ainda ser adicionadas uma velocidade de deriva devido ao vento e uma velocidade representativa do transporte difusivo.

3.1.1 Termo difusivo

O transporte turbulento é forçado pelos vórtices não resolvidos pelo modelo. O efeito destes vórtices, sobre os traçadores, depende da razão entre o tamanho dos vórtices e dos traçadores. Os vórtices maiores que os traçadores induzem um movimento aleatório ao traçador, como está esquematizado na Figura 16. Vórtices mais pequenos que os traçadores originam entrada de matéria para dentro do traçador, aumentando o seu volume e a sua massa de acordo com a concentração do meio envolvente (Figura 17).

3.1.2 Deslocamento aleatório

O movimento aleatório é calculado recorrendo ao procedimento adoptado por Sullivan, 1971, e por Allen, 1982. Este movimento é calculado utilizando o comprimento de mistura e o desvio padrão da velocidade turbulenta, obtidos a partir do fecho turbulento adoptado no modelo hidrodinâmico. Os traçadores mantêm a velocidade aleatória ou turbulenta durante o tempo necessário para percorrer o comprimento de mistura.

Figura 16- Movimento aleatório forçado por vórtices maiores que o traçador (círculo cinzento).

O método utilizado para calcular o deslocamento aleatório dos traçadores admite Ds igual ao comprimento de mistura e Dt igual ao tempo que o traçador demora a percorrer Ds. Nestas condições, a velocidade aleatória passa a ser u’=Ds/Dt. Para ser consistente, a metodologia random walk deve permitir que os traçadores mantenham a sua velocidade aleatória durante o período anteriormente referido que, em condições normais, é diferente do passo temporal do modelo hidrodinâmico.

Allen (1982) calcula a dispersão de uma pluma, impondo um movimento aleatório, igual em módulo ao comprimento de mistura e com igual probabilidade de ser positivo ou negativo. O tempo, durante o qual um traçador faz um salto aleatório, é igual ao comprimento de mistura a dividir pelo desvio padrão da velocidade turbulenta, . A velocidade aleatória é imposta como função das condições locais de turbulência. O modelo de traçadores admite turbulência isotrópica no plano horizontal, mas na vertical a dispersão anisotrópica é simulada explicitamente.

Na horizontal o comprimento de mistura é independente da direcção que o traçador toma no processo aleatório, mas na vertical o valor do comprimento mistura depende da trajectória aleatória ascendente ou descendente do traçador. Desta forma é possível simular o efeito da estratificação na mistura vertical e simular com modelos deste tipo, acoplados a modelos de turbulência, a produção primária em oceano aberto (Miranda et al., 1999).

A abordagem que utiliza o conceito de comprimento de mistura e de desvio padrão da velocidade turbulenta visa simular a trajectória turbulenta dos traçadores de uma forma fisicamente realista. Se se considerar um meio onde o fluxo de massa segundo x é apenas forçado pela turbulência e se emitir um conjunto de traçadores num ponto x=0, a taxa de dispersão destes pode ser escrita na forma (Tennekes, 1972):

A taxa de dispersão não é mais que a taxa a que a variância da variável estatística, distância à origem, varia no tempo. A correlação entre x e u’ de um traçador em movimento é muito baixa para lá do comprimento de mistura, isto é, para x>L . Assim sendo, o valor de pode ser estimado como sendo da ordem de u_TL, em que é a raiz quadrada da variância da velocidade turbulenta segundo x e L o comprimento de mistura.

Na metodologia random walk o comprimento de mistura (L) não é mais que a distância que o traçador tem que percorrer para “esquecer” a sua velocidade aleatória (ou turbulenta) inicial u’, que é reinicializada recorrendo a uma distribuição estatística de média nula e variância u_T², sempre que o traçador percorre a distância L. Num meio isotrópico L tem um valor constante mas, para meios estratificados e junto de fronteiras sólidas, este valor é variável.

Nesta metodologia, o intervalo de tempo que separa dois deslocamentos aleatórios não é uma constante especificada pelo utilizador, mas também uma variável aleatória uma vez que Dt=L/u_T , o que pode levantar problemas de ordem prática, especialmente para escoamentos com comprimento de mistura fortemente variável. Em zonas onde L é muito pequeno (por exemplo junto a uma fronteira sólida) Dt é igualmente pequeno tornando o algoritmo demasiado lento. Por vezes, com o objectivo de aumentar a eficiência do algoritmo, é admitido que L e u_Ttomam valores constantes em todo o domínio o que indirectamente equivale a admitir Dt constante, uma vez que Dt=L/u_T.

3.1.3 Aumento do volume

Um aspecto que normalmente não é considerado nos modelos lagrangeanos é o transporte difusivo forçado por vórtices de menor dimensão que os próprios traçadores (cf. Figura 17).

Figura 17- Aumento do volume por vórtices mais pequenos que o traçador (círculo cinzento).

Este efeito pode ser simulado na forma de um aumento de volume do traçador, só fazendo no entanto sentido quantificá-lo, caso as dimensões do traçador sejam uma das propriedade simuladas.

Ozmidov postulou a hipótese de fornecimento de energia quase discreto ao oceano. De acordo com esta teoria, a injecção de energia no oceano, por fontes externas, está concentrada na vizinhança de três escalas características do escoamento: escala da circulação geral, escala das oscilações inerciais, escala da maré (~10 Km) e escala das ondas induzidas pelo vento (~10m). Um dos principais resultados deste postulado consiste em poder admitir-se que entre os pontos de injecção de energia, o coeficiente de difusão turbulento horizontal pode ser descrito pela “lei dos 4/3 de Kolmogorov”. Este resultado foi confirmado por diversos trabalhos experimentais, que mediram a dependência do coeficiente de difusão horizontal da escala característica (Ozmidov, 1990)

Considerando L como uma dimensão característica dum traçador, para condições de isotropia local, o coeficiente de difusão pode ser descrito pela expressão K=aL^b. Pelo postulado de Ozmidov, a é uma constante proporcional à raiz cúbica da taxa de dissipação da energia cinética turbulenta, b é uma constante que, para condições de isotropia, é igual a 4/3 ( lei dos 4/3 de Kolmogorov).

Para condições de isotropia, aplicando a lei de Kolmogorov à solução analítica da equação diferencial de difusão tridimensional, correspondente a uma emissão pontual na origem x_i=0, se pode escrever (Fischer, 1979)

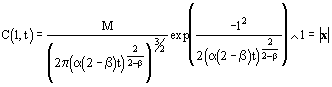
Considerando D como o diâmetro onde se concentra aproximadamente 95% da massa do traçador então .

Caso se entenda igualmente D como a dimensão característica do traçador, L»D, então se pode dizer que o respectivo volume é VµL³µt^3/(2-^b⁾. Em conclusão, para condições de isotropia, a taxa de variação do volume pode ser descrita como sendo .

Por razões de simplicidade e tendo em conta a elevada incerteza associada ao valor de b se assumiu que este vale 2 e portanto:

T_vol200- é uma constante e corresponde ao tempo que um traçador demora a duplicar de volume (parâmetro de calibração)

Esta equação é resolvida recorrendo a uma discretização explícita, a qual é mais estável que a implícita pois K_vol é sempre positivo.

O utilizador pode ainda especificar um volume máximo a partir do qual o traçador é eliminado, isto é, um valor a partir do qual se considera que a concentração dentro do traçador é aproximadamente igual à concentração no meio não perturbado.

3.2 Fontes e Poços

O modelo lagrangeano visa, essencialmente, resolver o transporte advectivo e o transporte difusivo. Os termos fontes-poços são resolvidos por módulos separados, dos quais se destacam o módulo ecológico, que simula a dinâmica em cada traçador do zooplancton (consumo primário), do fitoplâncton (produção primária) e dos nutrientes (Rodrigues e Neves, 1996) e o módulo de hidrocarbonetos que simula as alterações das propriedades físico-químicas e o espalhamento por dispersão mecânica de manchas de hidrocarbonetos (Silva, 1997).

3.2.1 Inactivação bacteriológica

Nos modelos de qualidade da água, utilizados em Engenharia é frequente utilizar reacções de primeira ordem. É o caso da inactivação bacteriológica e a sedimentação e ressuspensão de sedimentos.

Apesar da estrutura simplista destes algoritmos, eles são uma ferramenta muito útil e versátil numa primeira abordagem a problemas de qualidade da água e de dispersão de sedimentos contaminados.

As águas residuais contêm uma grande variedade de microorganismos, alguns dos quais patogénicos cuja determinação directa requer complexas análises microbiológicas. Com o objectivo de facilitar a verificação da qualidade da água e de permitir assim implementar esquemas de análise de água que permitam monitorizar extensas áreas (ex: praias, barragens, rios), utilizam-se indicadores biológicos de fáceis medição, que permitem estimar indirectamente o grau de contaminação da água. A maioria das normas, estabelecidas pelas autoridades sanitárias e pelos organismos responsáveis pela qualidade da água dos meios receptores, referem-se a níveis máximos e aconselhados de concentração de indicadores biológicos. Os coliformes totais e fecais são os principais indicadores utilizados.

Na simulação da inactivação, admite-se, normalmente, que este segue uma reacção de primeira ordem:

K_B - taxa de inactivação;

T₉₀ - tempo necessário para que a concentração de bactérias seja reduzida em 90%;

C - concentração de bactérias.

Em primeira aproximação, se pode admitir que T₉₀ é um valor constante e da ordem das 4 horas. Caso se pretenda simular, com precisão, este processo, é necessário utilizar valores de T₉₀ que tenham em conta a variabilidade da radiação solar ao longo do dia.

3.2.2 Sedimentação/Ressuspensão

De modo a ser possível simular o processo de sedimentação a cada traçador se associou uma velocidade de queda que pode ser dada directamente ou calculada a partir dum diâmetro característico, d, recorrendo às equações que calculam a velocidade de queda, w_s, de partículas não-esféricas propostas por Rijn (1989).

O traçador, ao chegar ao fundo, sedimenta somente se a tensão de corte do escoamento for inferior a uma tensão crítica de sedimentação, t_{sedimentação}, que é especificada pelo utilizador.

Por outro lado, se a tensão do escoamento for superior a uma tensão crítica de erosão (ou ressuspensão) , t_erosão>t_{sedimentação}, os traçadores, até então sedimentados, voltam a ser recolocados na coluna de água. Uma vez que o processo de ressuspensão é extremamente complexo, no caso dos estuários os sedimentos podem ser ressuspendidos alguns centímetros ou alguns metros, se optou por um critério de recolocar os traçadores aleatoriamente na coluna de água, no caso de haver condições de ressuspensão. O algoritmo simplificado, que simula o processo de ressuspensão, só pode ser aplicado a águas pouco profundas e bem misturadas.

3.2.3 Qualidade da Água

Os processos de qualidade da água (ou pelágicos) são simulados recorrendo a formulação proposta pela EPA (1985). Esta formulação foi implementada por Miranda (1999) no sistema Mohid, tendo por base a tese de mestrado de Rodrigues (1997) e de doutoramento de Portela (1996).

Os processos de qualidade da água são contabilizados na forma de termos de fonte e poço associados ao ciclo de carbono, fósforo e azoto. As propriedades que são alteradas por estes processos são designadamente o fitoplâncton, o zooplâncton, o CBO, o oxigénio, a amónia, o nitrato, o nitrito, o azoto orgânico particulado e o azoto orgânico dissolvido refractário e não-refractário, o fósforo orgânico e inorgânico.

3.3 Hidrocarbonetos

3.3.1 Introdução

A primeira versão de modelação numérica de hidrocarbonetos incluída no sistema MOHID foi feita no âmbito de uma tese de Mestrado (Silva, 1997). Este trabalho tinha como base os processos de espalhamento desenvolvido para o modelo MU-SLICK (Management Unit of the Mathematical Model of the North Sea and Scheldt Estuary) e os módulos de hidrodinâmica e transporte do sistema MOHID. A revisão completa do estado de arte referente as derrames de hidrocarbonetos, tal como a implantação da descrição matemática do transporte, do espalhamento natural e do envelhecimento dos hidrocarbonetos foram efectuados no âmbito daquela tese.

O módulo do sistema Mohid que resultou deste trabalho foi designado OilSpill. Uma segunda tese de mestrado efetuada com base no sistema Mohid (Costa, 1999) contém comparação entre vários modelos de análise e uma validação do modelo por comparação com dois acidentes ocorridos frente a costa portuguesa.

Atualmente, a simulação dos hidrocarbonetos com o sistema Mohid, é feita recorrendo ao modelo lagrangeano descrito nas seções anteriores deste capítulo. O módulo está adaptado para prever o comportamento de manchas em zonas costeiras simulando o espalhamento, as alterações das propriedades do óleo e diversos processos de envelhecimento, permitindo ainda o recurso a formulações alternativas opcionais.

Assim, o módulo tem em conta a evaporação (através da aproximação a pseudo-componentes –Yang & Wang 1977 e Payne et al. 1984), dispersão na coluna de água (podem ser utilizadas duas formulações diferentes – Delvigne & Sweeney 1988 e Mackay et al. 1980), emulsificação (opção entre as formulações de Rasmussen 1985 e Mackay et al. 1980) e dissolução (utilizando um método proposto por Cohen et al. 1980 e posteriormente actualizado por Huang & Monastero 1982).

São igualmente consideradas as alterações nas propriedades do óleo, nomeadamente no que se refere à densidade, que recorre à formulação utilizada pelo modelo ADIOS (NOAA 1994), e à viscosidade em que o algoritmo resulta da combinação das equações de Mooney 1951 e Mackay et al. 1980).

Nas secções seguintes são descritos os processos mais importantes ligados à deriva e destino final de manchas de hidrocarbonetos.

3.3.2 Espalhamento

Pode definir-se o espalhamento natural do óleo como o aumento da área da mancha devido à tendência que o óleo tem para se espalhar em água parada. Esta tendência é explicada pelas forças gravítica e tensão superficial, e contrariada pelo efeito inercial e viscosidade interfacial (óleo-água). Fay (1969) analisou este balanço de forças, assumindo que a mancha é circular e que a espessura do óleo na mancha é homogénea.

Nos primeiros minutos após o derrame, o espalhamento é, provavelmente, o processo predominante. Após algum tempo, e mediante a existência de vento forte, mar agitado e efeito das correntes, a mancha pode ser deformada, fragmentada e dispersa. Nestas condições, a aproximação de Fay torna-se inaplicável. Contudo, numa fase inicial do derrame, o cálculo da área da mancha pode ser estimado pela teoria de Fay ou outra teoria modificada, até porque a área é um parâmetro importante não só para o desenvolvimento de estratégias de defesa e contenção da mancha, mas também porque alguns processos de envelhecimento (como a evaporação, por exemplo) dependem directamente da área superficial ocupada.

Assim, segundo Fay, o espalhamento pode ser dividido em três fases, cada uma delas dominada por duas forças. Imediatamente após o derrame, o espalhamento é comandado pelas forças gravíticas – trata-se da fase gravítica-inércia. Após um período de tempo curto segue-se a fase gravítica-viscosa, em que a força gravítica é balanceada pela viscosidade interfacial óleo-água. Quando a espessura da mancha é muito pequena, a força gravítica deixa de ser importante, sendo o espalhamento dominado pelas forças de tensão superficial, e contrariado pela viscosidade interfacial – esta é a fase tensão superficial-viscosa.

A equação de Fay que descreve o balanço das forças acima mencionado é a seguinte:

onde:

R - raio da mancha assumindo um espalhamento axissimétrico

r_w- densidade da água

r_o- densidade do óleo

s- tensão interfacial oleo-água

g- aceleração da gravidade

t- tempo após o derrame

n_w- viscosidade cinemática da água

h- espessura da mancha

a₁, a₂ e a₃ são constantes empíricas adimensionais, que podem ser estimadas como sendo a₁=0.42, a₂=1.64, a₃=0.86, segundo Stolzenbach (1977).

As soluções dessa mesma equação para as três fases assumem as seguintes formas, com todas as unidades no Sistema Internacional:

Fase de espalhamento	L	R	D
Gravítica-inércia
Gravítica-viscosa
Tensão superficial-viscosa

L - comprimento característico da mancha para um espalhamento unidimensional

D - o coeficiente de difusão, muitas vezes utilizado para cálculo do espalhamento com base em modelos trajectórias de partículas Lagrangeanas.

D = (r_w-r_o)/r_w

V- volume do óleo derramado

A = 0.5V / unidade de comprimento da mancha

k₁, k₂ e k₃assumem diferentes valores por diferentes autores. Os valores recomendados (Flores et al, 1998) são, respectivamente, 0.57, 0.725 e 0.5.

Uma vez que a fase inicial é muito curta, muitas vezes não chega sequer a ser modelada directamente, sendo hábito calcular a área (A₀) e o tempo (t₀) em que esta fase termina, iniciando-se a fase gravítica-viscosa:

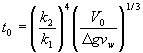
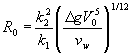
A área no final da primeira fase é, assim, muitas vezes assumida como a área inicial da mancha.

Para além disso, a terceira fase é também frequentemente inaplicável, uma vez que esta fase só se inicia quando a mancha já é muito fina, resultando muitas vezes numa divisão em pequenas manchas devido aos efeitos do vento e vagas. Desta forma, os pressupostos de Fay não são satisfeitos, visto que a mancha deixa de ser única.

Portanto, é comum utilizar apenas a fase gravítica-viscosa para calcular o espalhamento, assumindo que quando a espessura da mancha decresce até um determinado valor, o espalhamento termina. Mackay et al. (1980) recomendou um valor de 0.1 mm, valor este que foi utilizado no modelo ADIOS da NOAA (1994). No modelo de Reed (1989) esse mesmo valor é utilizado para crudes pesados, enquanto que para as substâncias menos viscosas assume-se o valor de 0.01 mm.

Uma vez que as fórmulas de Fay subestimam a taxa de espalhamento para a fase gravítica-viscosa (pois não consideram o efeito do vento e a turbulência associada), surgiram algumas correcções empíricas. Lehr et al. (1984) propôs a seguinte formulação modificada de Fay:

em que W é a velocidade do vento em nós, V é o volume em barris, t é o tempo em minutos e A_s é a área da mancha em m².

Outra formulação modificada de Fay para o espalhamento na fase gravítica-viscosa foi proposta por Mackay et al.(1980) e utilizada em diversos modelos:

sendo K_M uma constante empírica com um valor de 150 s^-1.

3.3.3 Evaporação

O processo da evaporação é um processo bastante importante, que ocorre desde o início do derrame. Quando o óleo é derramado, os componentes que possuem ponto de ebulição mais baixo (mais voláteis) são rapidamente volatilizados, reduzindo assim o volume e a massa da mancha que permanece na água. Durante as primeiras 24 horas após o derrame, a maior parte dos óleos-crude perdem aproximadamente 25-30% dos seus componentes mais leves. Os derrames de hidrocarbonetos mais leves podem ter o seu volume reduzido em 40% em poucas horas, apenas devido à evaporação (Costa, 1999). A evaporação destes componentes mais voláteis aumenta a densidade e viscosidade da mancha de óleo, podendo os compostos mais pesados continuar a sofrer outros processos de envelhecimento. A evaporação é, portanto, o primeiro processo envolvido na remoção de óleo da superfície da água. À medida que o óleo continua a envelhecer, e especialmente se se formarem emulsões água-no-óleo, a evaporação vai diminuindo progressivamente.

A taxa e extensão da evaporação dependem de diversos factores, tais como as fracções com baixo ponto de ebulição, área superficial e espessura da mancha, pressões de vapor do óleo e coeficiente de transferência de massa, que por seu turno são funções da composição do óleo, velocidade do vento, estado do mar e temperatura do ar e da água.

Diferentes algoritmos podem ser utilizados para o cálculo da taxa de evaporação. Entre os mais conhecidos encontram-se o modelo de pseudo-componentes (Yang & Wang, 1977 e Payne et al., 1984) e o modelo analítico, também conhecido como o modelo de exposição evaporativa (Stiver & Mackay, 1984).

A aproximação de pseudo-componentes assume que os óleos-crude e os produtos refinados são constituídos por uma mistura de componentes discretos independentes, designados por pseudo-componentes, em que cada um deles é tratado como sendo uma substância singular com uma pressão de vapor associada. Os pseudo-componentes e o respectivo ponto de ebulição são geralmente determinados com base no método da destilação.

A taxa de evaporação volumétrica para cada pseudo-componente i pode ser calculada pela seguinte equação:

Em que V_eⁱé o volume evaporado da fracção i, t é o tempo, K_eⁱé o coeficiente de transferência de massa, P_i^sat é a pressão de vapor da fracção considerada, R é a constante universal dos gases perfeitos, T é a temperatura do óleo, é o volume molar relativo da fracção i, A_sé a área da mancha e c_i é a fracção molar do componente i. Por vezes, é utilizada alternativamente a fracção em volume.

O volume molar relativo de cada pseudo-componente é encontrado a partir de uma correlação entre o volume molar e o ponto de ebulição para uma série de alcanos (C₃-C₂₀):

A pressão de vapor saturado de cada pseudo-componente pode ser determinada com base na equação de Antoine:

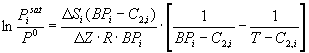
em que P⁰é a pressão atmosférica, DS_i é a variação na entropia resultante da vaporização da fracção i, DZ é o factor de compressibilidade (assume-se que DZ = 0,97), BP_i é o ponto de ebulição do componente i, e C_2,i é um coeficiente empírico. Assim,

O coeficiente de transferência de massa pode assumir diferentes formulações. Segundo Mackay e Matsugu (1973):

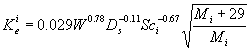
em que nesta equação W é a velocidade do vento em m.h^-1, D_s é o diâmetro da mancha (m), Sc_i é o número de Schmidt para a fracção i (adimensional) e M_i é a massa molecular de cada fracção (Kg.m³). As unidades de K_eⁱ são, portanto, em m.h^-1

Mais tarde Buchanan e Hurford (1988) propuseram uma formulação mais simples:

O valor de 2.5x10^-3 não é consensual em toda a literatura, podendo variar entre 1.5 x10^-3 e 5.0 x10^-3.

O método da exposição evaporativa pode ser expresso por:

A e B são constantes empíricas, T_o é o ponto de ebulição inicial e T_G é o gradiente da curva de destilação. Todas estas propriedades dependem do tipo de óleo. Caso estes valores sejam desconhecidos, poderão ser aproximados, sendo T_o e T_G estimadoscom base na densidade API, de acordo com a versão 1.1 do modelo ADIOS (NOAA 1994):

A = 6.3 B = 10.3

Para óleos-crude:

Para produtos refinados:

O método dos pseudo-componentes fornece resultados bastante razoáveis, no entanto requer maior informação sobre o óleo. Para além disso, o facto das fracções serem determinadas com base na temperatura de destilação poderá conduzir a alguns desvios à realidade, uma vez que compostos diferentes podem possuir a mesma temperatura de ebulição, como por exemplo alcanos, naftenos e aromáticos.

Quanto ao método da exposição evaporativa, este não requer informação sobre a composição do óleo. Contudo, os resultados obtidos só são válidos para as primeiras 8 horas após o derrame, uma vez que após este período o método fornece valores demasiado elevados.

Neste momento, o cálculo da evaporação no sistema MOHID é efectuado recorrendo ao modelo dos pseudo-componentes

3.3.4 Dispersão

A dispersão vertical é um processo físico em que as gotículas de óleo são transportadas a partir da superfície do mar para a coluna de água, sobretudo devido à rebentação das ondas. Essas gotículas podem ter dimensões variáveis, sendo que as mais pequenas não voltam à superfície devido à turbulência natural da água, difundindo-se na coluna de água.

Este processo é influenciado por três factores essenciais: viscosidade do óleo, temperaturas da água e do ar e estado do mar.

Quanto maior for a viscosidade do produto, maior é a possibilidade de se formarem espessas camadas de óleo na superfície da água, e assim diminuir a dispersão do mesmo na água, ao contrário dos hidrocarbonetos menos viscosos que facilmente se podem dispersar completamente ao fim de alguns dias.

As temperaturas da água e do ar também podem inibir a dispersão, caso sejam inferiores ao ponto de fluidez.

O estado do mar é associado à energia da rebentação das ondas. Assim, em derrames de óleo durante tempestades, a dispersão poderá ser o principal mecanismo de remoção de óleo da superfície, enquanto que em condições meteorológicas normais a evaporação será mais significativa, apesar da dispersão poder continuar a ter alguma relevância.

Estudos mais recentes demonstraram que a presença de quantidades significativas de asfaltenos retardam o processo de dispersão do óleo (Fingas et al., 1993).

Delvigne e Sweeney (1988) desenvolveram uma série de estudos laboratoriais acerca da dispersão natural do óleo. Com base nos resultados experimentais obtidos, desenvolveram uma relação empírica para a taxa de dispersão do óleo para a coluna de água devida à rebentação das ondas:

em que:

d₀ é o diâmetro das partículas,

Dd é o intervalo de diâmetros das partículas,

c_oilé um parâmetro determinado experimentalmente, e que depende do tipo de óleo,

D_ba é a energia de dissipação das ondas por unidade de área superficial, que pode ser calculada da seguinte forma:

H_rms, é determinada por:

sendo H₀ a altura da onda.

F_wc é a fracção de superfície de mar atingida pela rebentação das ondas por unidade de tempo, dada por:

onde C_b=0,032 s.m^-1e W_i é a velocidade do vento para iniciar o rompimento (5 m.s^-1). T_wé o período da onda.

Caso a altura e período de onda não sejam conhecidos, estes poderão ser determinados empiricamente, com base na velocidade do vento, de acordo com a formulação utilizada no modelo ADIOS (NOAA 1994):

Uma vez que a energia turbulenta é de difícil determinação, existem outros algoritmos simplificados que parametrizam o processo de dispersão em função do quadrado da velocidade do vento. Entre eles, encontra-se a formulação utilizada por Mackay et al. (1973):

Esta formulação determina a taxa de transferência de massa por hora, em que m_oil é a massa de óleo que permanece à superfície, m é a viscosidade dinâmica do óleo (cP), h é a espessura da mancha (cm) e, W é a velocidade do vento (m.s¹) e s é a tensão interfacial óleo-água (dyne.cm^-1).

No sistema MOHID, os algoritmos programados permitem a previsão da dispersão através das duas formulações referidas anteriormente, consoante a opção do utilizador.

3.4 Emissão dos traçadores

No que concerne ao tempo, a emissão dos traçadores pode ser dividida em duas grandes classes instantânea ou contínua. Na primeira é apenas necessário definir a localização e a massa emitida, enquanto na segunda, em vez de massa é necessário definir uma vazão mássica que pode ser constante ou variável. Se o utilizador optar por uma vazão variável é necessário definir uma série temporal que indique a sua variação em função da data.

Quanto à localização pode-se dividir em pontual, por caixas e acidente. No caso da emissão pontual é apenas necessário definir as coordenadas geográficas da emissão, enquanto na emissão por caixas o utilizador tem que definir um polígono onde é efetuada a emissão (Figura 18).

No caso da emissão que se designou de acidente é também dada a localização geográfica, mais o volume emitido e a espessura inicial. Neste caso, o modelo distribui, de uma forma circular as partículas em torno da localização pontual definida.

Estes são tipos de emissão principais, mas podem ser efectuadas emissões híbridas. Por exemplo, para simular uma derrame de um petroleiro de uma forma realista é possível fazer uma emissão que, no instante inicial, é do tipo do acidente no espaço e instantânea no tempo (rombo instantâneo do casco do navio) se considerando que, após o derrame inicial, a emissão é feita pontualmente no espaço em contínuo no tempo (derrame lento de crude ainda armazenado nos tanques do navio).

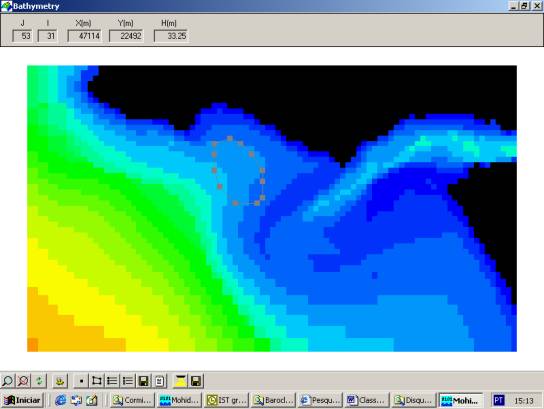
Figura 18 – Definição dos limites de um derrame, emissão por caixas.

3.5 Condições de Fronteira

Neste modelo são considerados dois tipos de fronteira: fronteiras com água e com terra. Para as fronteiras com água é adoptado o critério de eliminação do traçador, caso este saia do domínio. Se o traçador for arrastado para um ponto de terra, o utilizador pode optar na entrada de dados, por recolocar o traçador na sua posição imediatamente anterior ou admitir que o traçador fica retido na totalidade ou parcialmente na linha de costa. O utilizador pode ainda optar por considerar que uma destas opções é tomada pelo modelo função do tipo de costa. No caso dos hidrocarbonetos a primeira opção é normalmente adoptada em costas rochosas e a segunda em costas de areia.

4 Interface Gráfica do modelo Mohid

O modelo Mohid tem uma interface gráfica que permite ao utilizador gerir os dados de entrada do modelo, executar o programa e analisar os resultados produzidos. Esta interface foi escrita em Fortran e utiliza:

· as rotinas do modelo Mohid para a leitura e validação dos dados de entrada;

· as bibliotecas do MS Windows SDK (Software Development Kit) para a geração de janelas;

· as bibliotecas do OpenGL (Open Graphics Language) para a visualização dos resultados.

A programação da interface segue os mesmos conceitos da programação por objectos já utilizados na programação do modelo Mohid e foi desenvolvido pelos mesmos autores do modelo Mohid. Este fato é importante de salientar, pois garante que em desenvolvimentos futuros será sempre fácil de manter a mesma interface gráfica sincronizada com o desenvolvimento do modelo.

A Mohid GUI foi desenhada para correr em ambientes WindowsNT e Windows 2000 e pode igualmente correr, com algumas limitações em outras plataformas.

4.1 Organização de um projecto

A partir da Mohid GUI, o utilizador tem a possibilidade de organizar o projecto em várias simulações que por sua vez são constituídas por vários Runs. A execução de um projecto normalmente será sempre constituída por mais do que uma simulação, sendo por isso a organização hierárquica a mais adequada. Cada Run necessita de ficheiros de dados e produz resultados para cada parte modular do programa utilizada. Os resultados produzidos podem ser sob a forma de ficheiros de continuação de cálculo, ficheiros com resultados em instantes pré-seleccionados em toda a malha e ficheiros de resultados do tipo séries temporais.

Para uma melhor organização de todos os ficheiros associados, a interface gráfica do modelo Mohid constrói automaticamente uma árvore de directorias, que permite ao utilizador, caso deseje, encontrar mais facilmente um dado ficheiro (a necessidade de encontrar um dado ficheiro é relativa, uma vez que a partir da interface gráfica o utilizador pode fazer todas as tarefas). Esta árvore de directorias é dividida na seguinte maneira:

· na directoria de topo reside o ficheiro que contém as informações sobre o projecto e um sub-directoria para cada simulação que faz parte do projecto;

· em cada sub-directoria são criadas três directorias, um que contém os ficheiros de dados das corridas, outro em que é executado o código do modelo e um terceiro no qual são guardados os resultados do modelo;

· cada Run de uma simulação é identificada por um ID e a partir desse ID são construídos os nomes dos ficheiros para cada parte modular do programa e um sub-directoria na directoria dos resultados que contêm os resultados das séries temporais;

· cada parte modular tem um ficheiro de entrada de dados, um ficheiro de resultados transientes com saídas das propriedades em toda a malha de cálculo e um ficheiro que serve para continuar posteriormente o cálculo.

Os nomes dos ficheiros de dados de entrada são construídos automaticamente da seguinte maneira: nome de parte modular do programa + _ + ID + .dat. Por exemplo o ficheiro de entrada de dados do módulo de turbulência será “Turbulence_5.dat”, caso o Run tenha o ID 5. Os ficheiros de resultados são construídos da mesma maneira, chamando-se por exemplo “TransienteTurbulence_5.hdf”.

De notar que este processo da geração de nomes de ficheiros, identificação por ID’s, criação de directorias e sub-directorias é automatizada pela interface gráfica do modelo Mohid. Na Figura 19 se mostra um exemplo deste tipo de organização. Neste caso o projecto é chamado “Estuaries” e é constituído por 12 simulações (Mira, Douro, Minho, etc.). Na Figura 19 são visíveis os Runs correspondentes ao estuário do Mira, estando actualmente o “Run_Particle” seleccionado. Na lista da direita aparecem as opções de cálculo para cada parte modular do programa (Model, Hydrodynamic, Bottom, etc.), sendo aí dada a opção ao utilizador de modificar os parâmetros de cálculo de cada uma das partes modulares referidas.

Figura 19: Organização hierárquica das corridas no modelo Mohid

4.2 Entrada de dados

A entrada de dados para modelos numéricos pode ser feita sob várias formas como, por exemplo, por interacção directa com o utilizador, em ficheiros de dados sequenciais ou em ficheiros com formato organizadas por tópicos.

A organização dos ficheiros de dados do modelo Mohid é fruto de uma experiência muita longa no desenvolvimento de ferramentas da família Mohid. É frequente nos modelos numéricos se falar em erros de programação, mas o fornecimento de dados pelo utilizador do modelo é normalmente uma das fontes de erros mais significativa. Estes erros podem ter duas origens: distracção do utilizador ao definir os dados ou desconhecimento das hipóteses e/ou dos conceitos que estão que estão na base do modelo. Se estas fontes de erros não são minimizadas, a operacionalidade do modelo não é garantida.

O modelo Mohid recebe todos os dados através de ficheiros em formato ASCII (American Standard Code for Information Exchange). Este formato é independente, tal como o modelo Mohid, do sistema operativo. Estes ficheiros são organizados por blocos de informação e por palavras-chaves, duma forma semelhante ao XML (Extensible Markup Language), e podem ser construídas num editor de texto (tipo “Notepad”) ou através da interface gráfica do modelo Mohid. No início do cálculo o modelo verifica a consistência entre os dados fornecidos.

A Figura 20 mostra um ficheiro de dados que é fornecido ao modelo Mohid. Neste caso trata-se dum ficheiro de descargas de água para o rio Tejo, associadas a uma temperatura e uma salinidade.

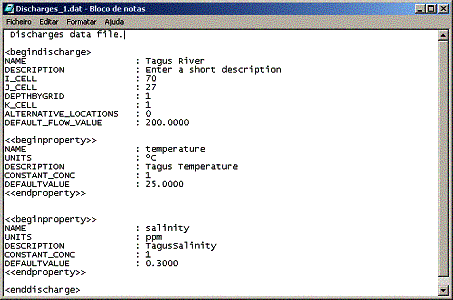
Figura 20: Ficheiro de dados do modelo Mohid

Na Figura 20 é facilmente visível a organização por blocos da informação (uma descarga é incorporada entre as linhas <begindischarge> e <enddischarge> e uma propriedade de água associada a uma descarga entre as linhas <<beginproperty>> e <<endproperty>>). Nesta figura é igualmente visível o conceito de palavra-chave (keyword). Qualquer valor fornecido ao modelo Mohid é precedido por uma palavra-chave, como por exemplo a palavra-chave “Default_Flow_Value”.

Como já referido anteriormente, o utilizador tem a possibilidade de construir estes ficheiros a partir da interface gráfica do modelo Mohid. A Figura 21 mostra a interface gráfica relativo ao ficheiro de dados da Figura 20.

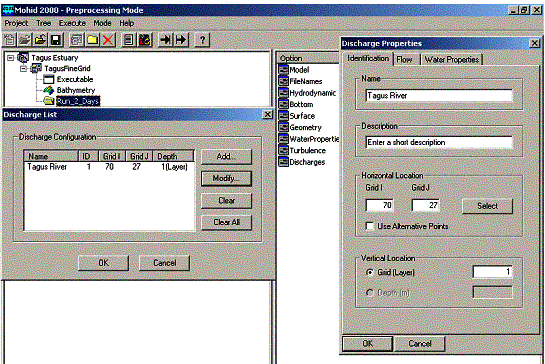
Figura 21: Construção de um ficheiro de dados a partir da GUI

Todas as partes modulares do modelo Mohid têm a mesma filosofia na construção dos ficheiros de dados. Em todas as partes modulares as palavras-chave com o mesmo sentido têm o mesmo nome. Se, por exemplo, o utilizador quer especificar o intervalo entre saídas de resultados em toda a grelha, a palavra-chave é sempre OUTPUT_TIME, independentemente da parte modular do programa, dando assim uma consistência adicional ao modelo (mais informações sobre a saída de resultados serão fornecidas mais à frente).

Além dos ficheiros de dados numéricos acima descritos, que indicam ao modelo os parâmetros de cálculo, existem dados que têm ser fornecidos por intermédio de séries temporais ou de matrizes. Estes dados podem ser variados (dados meteorológicos, vazões de rios, derrames acidentais, etc.), e podem ser fornecidos no formato 1D, 2D ou 3D.

Ainda existe a possibilidade destes dados serem variáveis ou não no tempo. O modelo Mohid utiliza para estes casos sempre formatos muito parecidos, sendo assim mais fácil para o utilizador do modelo fornecer os dados correctos. A Figura 22 mostra um exemplo de um ficheiro com séries temporais que é lido pelo modelo Mohid. Neste caso trata-se do fornecimento de dados 1D que são variáveis no tempo. A partir das unidades do tempo (palavra-chave Time_Units) e da data inicial da série (palavra-chave Série_Initial_Data) o modelo constrói todos os dados necessários para o intervalo de execução. A interface gráfica do modelo Mohid é acompanhada por um ficheiro de MS Excel, que contém macros que ajudam o utilizador a escrever este tipo de ficheiro de dados.

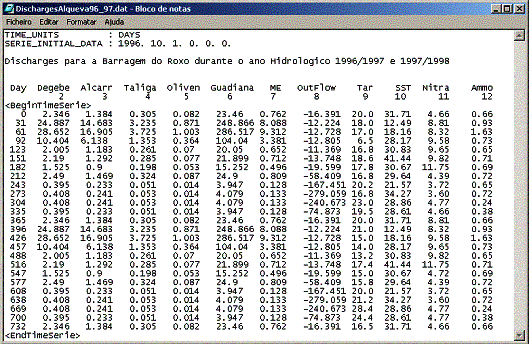
Figura 22: Fornecimento de séries temporais

Os dados que são fornecidos em matrizes têm um formato parecido com o formato indicado na Figura 22 e que é sempre igual para cada parte modular do programa Mohid.

4.3 Saída de resultados

A saída de resultados do modelo pode ser especificada pelo utilizador, através dos ficheiros de dados. Como já referido anteriormente existem dois tipos de resultados no modelo Mohid. Para cada parte modular do programa, existe a hipótese de escrever os resultados para toda a grelha no formato HDF ou na forma de séries temporais no formato ASCII. O intervalo entre as saídas dos resultados pode ser especificado pelo utilizador, quer para as séries temporais, quer para os resultados em toda a malha.

O formato dos ficheiros de resultados na forma de séries temporais, é igual ao formato de entrada de séries temporais (como indicado na Figura 22). A interface gráfica do modelo Mohid é acompanhada por uma macro que permite importar estes resultados numa folha de Excel. Igualmente é possível abrir estes resultados directamente no Excel a partir da interface gráfica.

O formato adoptado para a escrita de valores em toda a malha, o HDF, tem várias vantagens, nomeadamente:

· é independente do sistema operativo em que formam escritos os ficheiros;

· necessita pouco espaço no disco, pois utiliza internamente um algoritmo de compressão;

· é auto descritivo;

· é um formato com um universo de utilização muito alargado.

O desenvolvimento e a manutenção deste formato é da responsabilidade da NCSA (National Center for Supercomputing Applications dos EUA).

4.4 Visualização dos resultados

Qualquer pessoa ligada a modelação sabe que a visualização dos resultados produzidos por um modelo numérico pode ser um processo demorado e trabalhoso. Com o objectivo de facilitar a análise dos resultados, a Mohid GUI incorpora um pós- processador que se pode dividir duas partes. Existe uma parte em que o utilizador pode seleccionar a informação que pretende representar e outra parte a da visualização propriamente dita.

A selecção da informação é muito facilitada pelo fato de que os ficheiros transitórios de resultados são escritos em HDF. Ao abrir um ficheiro de HDF a Mohid GUI mostra a árvore de informação contida neste ficheiro. Na Figura 23 são apresentados dois ficheiros HDF, abertos com o browser da Mohid GUI e as hipóteses para o utilizador ver as propriedades do cada conjunto de resultados, tal como a hipótese de exportar os dados para outros formatos.

Figura 23: Opções do Browser do ficheiros transientes

Com os resultados disponíveis, o utilizador tem a hipótese de gerar mapas de cores, linhas de contorno, mapas de vectores, traçadores lagrangeanos ou diferenças entre campos de cores. A representação pode ser feita da malha inteira ou de zooms da malha em qualquer plano do modelo tridimensional (XY, XZ ou YZ), conforme as especificações do utilizador. Existe a possibilidade de sobrepor vários mapas ao mesmo tempo. Para cada tipo de mapas, o utilizador tem a possibilidade de escolher entre vários tipos:

· os mapas de cores podem ser representados em escalas de cores contínuas ou discretas, deixando ao utilizador a liberdade de escolher o tipo de escala a utilizar (tons de azul, tons do arco íris, etc.). É possível representar qualquer escala de cores imaginária;

· as linhas de contorno são um bom complemento para as escalas de cores, ou podem representar uma outra propriedade, de modo a cruzar a informação representando no campo de cores a evolução da propriedade representada com as linhas de contorno;

· os mapas de vectores são indispensáveis para representar velocidades, pois permitem, numa forma fácil, representar a intensidade e a direção ao mesmo tempo. O utilizador da Mohid GUI tem a hipótese de escolher entre várias formas de representar os mapas de vectores;

· os traçadores lagrangeanos podem ser visualizados com diferentes escalas de cores ou com cor uniforme, permitindo ao mesmo tempo ao utilizador visualizar a história da trajectória, que é muito útil para as manchas de petróleo.

Após a selecção completa da informação a representar, o utilizador pode visualizar os resultados na tela ou gravar as imagens como ficheiros independentes no disco rígido. Um utilitário chamado “Sequencer” permite ao utilizador controlar a velocidade da representação na tela, ou seja controlar o tempo real versus o tempo simulado.

As figuras gravadas no disco rígido podem ser utilizados para fazer animação em formato “gif”, “avi” ou similares, recorrendo a programas disponíveis para este fim (por exemplo o Paint Shop Pro).

5 Referências

Descrição Geral

Adcroft A.J., Hill C.N., Marshall J., Representation of Topography by Shaved Cells in a Height Coordinate Ocean Model, Mon. Weather Rev. 125 (1997) 2293-2315.

Decyk, V. K., Norton, C. D. e Szymansky, B. - How to Express C++ Concepts in Fortran90.

Duffy, D. - From Chaos to Classes, McGraw-Hill: London, 1995.

Leitão, P. C. (1997) – Modelo de Dispersão Lagrangeano Tridimensional. Tese de Mestrado, Universidade Técnica de Lisboa, Instituto Superior Técnico

Miranda, R., Braunschweig, F., Leitão, P. Neves, R., Martins, F. and Santos, A. (2000) – Mohid 2000, A Costal integrated object oriened model. Hydraulic Engineering Software VIII, WIT Press

Neves, R. J. J. (1985) - Étude Experimentale et Modélisation des Circulations Trasitoire et Résiduelle dans l’Estuaire du Sado. Ph. D. Thesis, Univ. Liège

Silva, S. B. (1997) – Modelação Numérica de Derrames de Hidrocarbonetos no Mar: Aproximação Lagrangeana do Transporte. Universidade Técnica de Lisboa, Instituto Superior Técnico.

Modelo Hidrodinâmico

Abbott, M.B., A. Damsgaardand & G.S. Rodenhuis, 1973. System 21, Jupiter, a design system for two-dimensional nearly-horizontal flows. J. Hyd. Res., 1, p. 1-28.

Adcroft A.J., Hill C.N., Marshall J., Representation of Topography by Shaved Cells in a Height Coordinate Ocean Model, Mon. Weather Rev. 125 (1997) 2293-2315.

Arakawa, A. and V. R. Lamb, 1977: Computational design of the basic dynamical processes of the UCLA general circulation model. Methods in Computational Physics, 17, 174-265.

Arhan, M., Colin de Verdière, A, and L. Mémery, The Eastern boundary of the subtropical North Atlantic, J. Phys. Oceanogr., 24, 1295-1316, 1994

Blumberg, A.F. and L.H. Kantha, 1985. Open boundary condition for circulation models. J. of Hydraulic Engineering, ASCE, 111, 237-2555.

Braunschweig, 2001. Generalização de um modelo de circulação costeira para Albufeiras. Tese de mestrado em Ecologia, Gestão e Modelação dos Recursos Marinhos. Universidade Técnica de Lisboa. Instituto Superior Técnico. Lisboa, 2001.

Chippada S., Dawson C., Wheeler M., A godonov-type finite volume method for the system of shallow water equations, Computer methods in applied mechanics and engineering. 151(01):105-130. 1998

Choi H. B., D. G. Kim e D. H. Kim (1997). A Numerical Tidal Model for the Southeast Asian Seas. Journal of Korean Society of Coastal and Ocean Engineers. Vol. 9, No. 2, pp. 63-73, june 1997.

Coelho, H. S., R. J. J. Neves, M. White, P. C. Leitão e A. J. Santos. A circulation model for the western Iberia. Journal of Marine Systems. In press

Deleersnijder E. e J.-M. Beckers, 1992, On the use of the sigma-coordinate system in regions of large bathymetric variations, Journal of Marine Systems, 3, 381-390

Ferziger, J., Perić, M., Computational methods for fluid dynamics, Springer, 1995.

Flather, R.A., 1976: A tidal model of the nothweast European continental shelf. Mem. Soc. R. Sci. Liege, Ser. 6(10), 141-164.

Hellerman, S. and M. Rosenstein, 1983. Normal monthly wind stress over the world ocean with error estimates. Journal of Physical Oceanography, 13, 1,093-1,104.

Kantha, L. H. and C. A. Clayson, 2000. Numerical Models of Oceans and Oceanic Processes. International Geophysics Series. Volume 66. Academic Press.

Le Provost, C., F. Lyard, J.M. Molines, M.L. Genco and F. Rabilloud, 1998. A Hydrodynamic Ocean Tide Model Improved by assimilating a satellite altimeter derived dataset. J. Geophys. Res. Vol. 103 N. C3, 1998.

Le Provost, C., M.L. Genco, F. Lyard, P. Vincent, and P. Canceil, Spectroscopy of the world ocean tides from a finite element hydrodynamic model, J. Geophys. Res., 99, 24,777-24,797, 1994.

Leendertsee J., Liu S., A three-dimensional turbulent energy model for non-homogeneous estuaries and coastal sea systems, in: Nihoul J. (Eds.), Hydrodynamics of Estuaries and Fjords, Elsevier, Amsterdam, 1978 pp. 387-405.

Leendertsee, J.J., 1967. Aspects of a computational model for long water wave propagation. Rand Corporation, Memorandum RH-5299-RR, Santa Monica.

Leendertsee, J.J., 1970. A water quality simulation model for well mixed estuaries and coastal seas. Rand Corporation, Memorandum RM-6230-RC , Santa Monica.

Levitus, S. and., T. P. Boyer, 1994. World Ocean Atlas 1994. Volume 4: NOAA Atlas NESDIS 4, 117pp.

Levitus, S., R. Burgett and T. P. Boyer, 1994. World Ocean Atlas 1994. Volumes 1 and 2: NOAA Atlas NESDIS 3, 99pp.

M. Ruiz-Villarreal1*, P. Montero1, J.J. Taboada1, R. Prego2, P.C. Leitão3 and V. Pérez-Villar1. Hydrodynamic Model Study of the Ria de Pontevedra under Estuarine Conditions. Estuarine and Coastal Shelf Science. In press.

Martins, F., R. Neves, P. Leitão e A. Silva, 2001. 3D modeling in the Sado estuary using a new generic coordinate approach. Oceanologica Acta, 24:S51-S62.

Martinsen, Eivind A. e Harald Engedahl: Implementation and testing of a lateral boundary scheme as an open boundary condition in a barotropic ocean model, Coastal Engineering, 11, 603-627, 1987.

Neves R., Leitão P., Braunschweig F., Martins F., Coelho H., Santos A., Miranda R.: The advantage of a generic coordinate approach for ocean modelling. Proceedings of the Eighth International Conference Hydraulic Engineering Software HYDROSOFT 2000,12-14 Junho 2000, Lisboa.

Neves, R.J.J. e Silva, A.J.R., 1991, An Extension of the Boussinesq Equations to Deep Water - Computer Modelling in Ocean Engng.,1991. A.S. Arcilla, M. Pastor, O.C. Zienkiewicz & B.A. Schrefler, eds. Balkema, Rotterdam, p. 301-309.

Neves, R.J.J., 1985. Étude experimentale et modélisation mathématique des circualtions transitoire et résiduelle dans l’Estuarie du Sado. Ph.D. Thesis, Université de Liège, Belgique.

Paillet, J. and H. Mercier, 1997. An inverse model of the eastern North Atlantic general circulation and thermocline ventilation. Deep Sea Res., 44 (8), 1293-1328.

Palma, E. D. and R. P. Matano, 1998: On the implementation of passive open boundary conditions for a general ciruclation model: The barotropic mode. Journal of Geophysical Research, 103,. 1319-1342..

Palma, E. D. and R. P. Matano: On the implementation of passive open boundary conditions for a general circulation model: The three-dimensional case. Journal of Geophysical Research, 105,. 8605-8627.

Roed, L.P.; Smedstad, O.M. (1984). Open boundary conditions for forced waves in a rotating fluid. SIAM Journal on Scientific and Statistical Computing, vol.5, no.2, p. 414-26, 1984.

Ruiz-Villarreal, M., 2000. Parameterization of turbulence in the ocean and application of a 3D baroclinic model to the Ria de Pontevedra PhD. Thesis. University of Santiago de Compostela.

Santos, A.J.P. & R.J.J. Neves, 1991. Radiative artificial boundaries in ocean barotropic models. Computer Modelling in Ocean Engng.,1991. A.S. Arcilla, M. Pastor, O.C. Zienkiewicz & B.A. Schrefler, eds. Balkema, Rotterdam, p. 373-383

Santos, A.J.P., 1995. Modelo hidrodinâmico tridimensional de circulação oceânica e estuarina. Tese de doutoramento. Instituto Superior Técnico, Universidade Técnica de Lisboa, 273 pp.,Lisboa.

Silva, A.J.R., 1991, Modelação Matemática Não Linear de Ondas de Superfície e de Correntes Litorais, Tese apresentada para obtenção do grau de Doutor em Engenharia Mecânica. IST, Lisboa.

Stelling, G.S., 1983. On the construction of computational methods for shallow water flow problems. Ph.D. Thesis, Tecnische Hoegeschool to Delft.

Stevens, D.P. (1991): The Open Boundary Condition in the United Kingdom Fine Resolution Antarctic Model. Journal of Physical Oceanography, 21, pp. 1494-1499.

Trenberth, K. E., W. G. Large and J. G. Olsen, 1990: The mean annual cycle in global wind stress. J. Phys. Oceanogr., 20, 1742-1760.

Vinokur, M., 1989. An analysis of finite-difference and finite-volume formulations of conservation laws. J. Comp. Phys., 81, p. 1-52.

Módulo de Deriva

Allen, C. M. (1982). Numerical simulation of contaminant dispersion in estuary flows. Proc. R. Soc. London. A 381, 179-194 (1982).

Bork, I. and Maier-Reimer, E. (1978) - On the Spreading of Power Plant Cooling Water in a Tidal River Applied to the River Elbe. Advances in Water Resources Vol. 1 No.3 1978

Buchanan I., N. Hurford (1988) - Methods for predicting the physical changes in oil spilt at sea. Oil & Chemical Pollution, 4(4), pp. 311-328

Cohen, Y., D. MacKay, W.Y.Shiu (1980). Mass transfer rates between oil slicks and water. The Canadian Journal of Chemical Engineering. Vol. 58.

Costa, M. V. (1991) - A Three-Dimensional Eulerian-Lagrangian Method for Predicting Plume Dispersion in Natural Waters - Diplôme d’Etudes Approfondies Européen en Modélisation de l’Environnement Marin - ERASMUS.

Costa, M. (1999) - Evolução de hidrocarbonetos derramados nas zonas costeiras e estuarinas. Dissertação de Mestrado, Faculdade de Ciências e Tecnologia, Universidade de Coimbra, Coimbra

Delvigne G.A.L., C.E. Sweeney (1998) - Natural Dispersion of Oil. Oil & Chemical Pollution. 4, pp. 281-310

Dippner, J. (1993) - A Lagrangian model of phytoplankton growth dynamics for the Northern Adriatic Sea. Continental Shelf Research. Vol. 13, No. 2/3, pp. 331-355, 1993.

Fay J.A. (1969) - The spread of oil slicks on a calm sea. Oil on the Sea, Plenum Press, NY, pp. 53-63

Fingas M.F., D.A. Kyle, E. Tennyson (1993) - Physical and Chemical Studies on Dispersants: The effect of Dispersant Amount and Energy. Proceedings of the Sixteenth Arctic and Marine Oil Spill Program Technical Seminar, Environment Canada, Ottawa, Ontario, pp. 861-876

Fischer, H. B. ; List, E. J. ; Koh, R. C. Y. ; Imberger, J. and Brooks, N. H. (1979) - Mixing in Inland and Coastal Waters. Academic Press, New York, U.S.A., 483p.

Flores H., A. Andreatta, G. Llona, and I. Saavedra (1998). Measurements of oil spill spreading in a wave tank using digital image processing. Oil and hydrocarbon spills, modeling, analysis and control, WIT Press, Southampton, UK, pp.165-173

Garcia-Martinez, Reinaldo, Henry Flores-Tovar (1999) - Computer Modeling of Oil Spill Trajectories with a High Accuracy Method. Spill Science & Technology Bulletin, Vol. 5, No.5/6, pp. 323-330

Huang, J.C., F.C. Monastero (1982). Review of the state-of-the-art of oil spill simulation models. Final Report submitted to the American Petroleum Institute.

Kelsey, A., Allen, C. M., Beven, K. J. and Carling, P. A. (1994) - Particle Tracking Model of Sediment Transport. Mixing and Transport in the Environment. Ed. WILEY, 419-442.

Kung, Chen-Shan, Huo-Hsu Su, Yi-Ching Chen, Yao-Li Teng Simulation of Oil Spills in a Harbor

Lehr, W.J., R.J. Fraga, M.S.Belen and H.M. Cikerge (1984). A new technique to estimate initial spill size using a modified Fay-type spreading formula, Marine Pollution Bulletin, 15(9), pp. 326-329

Leitão, P. C. (1997) – Modelo de Dispersão Lagrangeano Tridimensional. Tese de Mestrado, Universidade Técnica de Lisboa, Instituto Superior Técnico

Mackay D., R.S. Matsugu (1973) - Evaporation rates of liquid hydrocarbon spills on land and water. Canadian Journal Chemical Engineering, pp. 434-439

Mackay D., I. A. Buistt, R. Mascarenhas, S. Paterson (1980) - Oil spill processes and models. Environment Canada Manuscript Report No. EE-8, Ottawa, Ontario

Monteiro, A. J. , Neves, R. J. and Sousa, E. R. (1992) - Modelling Transport and Dispersion of Effluent Outfalls. Water Science and Technology WSTED4, Vol. 25, No. 9, p 143-154, 1992.

Mooney, M. (1951). The viscosity of a concentrated suspension of spherical partiles. Journal Colloidal Science, 10, 162-170

Neves, R. J. J. (1985) - Étude Experimentale et Modélisation des Circulations Trasitoire et Résiduelle dans l’Estuaire du Sado. Ph. D. Thesis, Univ. Liège

Neves, R. J. J. and Martins, F. A. (1996) - Modelação Lagrangeana dos processos de transporte na Ria Formosa. 5a Conferência Nacional sobre a Qualidade do Ambiente, Aveiro.

Mansur, L. , Price D. M. (1992). Oil-RW: A mathematical model for predicting oil spills trajectory and weathering. Hydraulic and Environmental Modelling: Coastal Waters. Proceedings of the Second International Conference on Hydraulic and Environmental Modelling of Coastal, Estuarine and River Waters, Volume 1, pp. 201 - 212.

Monteiro, A. J. (1995) - Dispersão de Efluentes Através de Exutores Submarinos. Uma contribuição para a modelação matemática. Universidade Técnica de Lisboa, Instituto Superior Técnico.

NOAA (1994). ADIOS^TM (Automated Data Inquiry for Oil Spills) user’s manual. Seattle: Hazardous Materials Response and Assessment Division, NOAA. Prepared for the U.S. Coast Guard Research and Development Center, Groton Connecticut, 50 pp.

Ozmidov, R. V. (1990) - Diffusion of Contaminants in the Ocean. Oceanographic Sciences Library, Kluwer Academic Publishers, 283 p.

Payne J.R., B.E. Kirstein, G.D. McNabb, J.L. Lambach, R. Redding, R.E. Jordan, W. Hom, C. De Oliveira, G.S. Smith, D.M. Baxter, R. Gaedel (1984) - Multivariate analysis of petroleum weathering in the marine environment – Sub arctic. Environment Assessment of the Alaska Continental Shelf. Final reports of the principal investigations, Vol. 22, US Dept. Commerce, NOAA/NOS/OAD. US Dept. Interior, MMS, Vol. II

Portela, L. (1996) - Modelação matemática de processos hidrodinâmicos e de qualidade da água no Estuário do Tejo. Dissertação para obtenção do grau de Doutor em engenharia do Ambiente, Instituto Superior Técnico, Universidade Técnica de Lisboa.

Rasmussen, D. (1985). Oil Spill Modelling – A tool for cleanup operations. Proc. 1985. Oil Spill Conference, American Petroleum Institute, pp. 243-249

Reed M. (1989) - The physical fates component of the natural resource damage assessment model system. Oil & Chemical Pollution, 5, pp. 99-123

Rijn, L. C. (1989) - Handbook Sediment Transport by Currents and Waves. Delft Hydraulics, Report H 461, June 1989.

Rodrigues, V., Neves, R. J. J. & Miranda, R (1996) - Modelação ecológica e da qualidade da água em zonas costeiras. 5a Conferência Nacional sobre a Qualidade do Ambiente, Aveiro.

Shiau, B. (1991). Computer modelling of oil pollutants transport on the water. Computer modellnig in Ocean Engineering: Vol. 91, pp. 467-475.

Silva, S. B. (1997) – Modelação Numérica de Derrames de Hidrocarbonetos no Mar: Aproximação Lagrangeana do Transporte. Universidade Técnica de Lisboa, Instituto Superior Técnico.

Stiver W., D. Mackay (1984) - Evaporation rate of spills of hydrocarbons and petroleum mixtures. Environmental Science and Technology, 18(11), pp. 834-840

Stolzenbach K.D., O.S. Madsen, E.E. Adams, A.M. Pollack and C.K. Cooper (1977) - A review and evaluation of basic techniques for predicting the behavior of surface oil slicks. MIT Sea Grant Program, Report No. 222, Massachusetts Institute of Technology, Cambridge, Massachusetts

Sullivan, P. J. (1971). Longitudinal dispersion within a two-dimensional turbulent shear flow. Journal Fluid Mech., vol. 49, part 3, pp. 551-576 (1971).

Tennekes H. e Lumley (1972) - A First Course in Turbulence. Edited by MIT Press.

Varlamov, Sergey M., Kazuko Abe (2000) - Oil Spill Initial Stage Spreading and Physical Properties Model. Reports of Research Institute for Applied Mechanics, Kyushu University, No. 119 pp. 89-101

Yang W. C., H. Wang (1977) - Modelling of oil evaporation in aqueous environment. Water Research, 11, pp. 879-887

Woods, J. D. and Onken, R. (1982) – Diurnal variation and primary production in the ocean – preliminary results of a Langrangian ensemble model. Journal of Plankton Research, 4, 3.

Miranda, R., R. Neves, H. Coelho, H. Martins, P. C. Leitão and A. Santos, 1999: Transport and Mixing Simulation Along the Continental Shelf Edge Using a Lagrangian Approach, Bol. Inst. Esp. Oceanogr., 15,39-60

Miranda, R. (1999) - Nitrogen biogeochemical cycle modeling in the North Atlantic ocean. . MsC. Thesis – IS, 1999, Lisbon.

EPA (1985) – Rates, constants, and kinetic formulations in surface water quality modeling (2nd ed.). USEPA, Report EPA/600/3-85/040.